Las velocidades de evolución de IDPs son modeladas por los ensembles conformacionales (*)
Julia MarchettiDOI: https://doi.org/10.48160/25913530di17.205
* Originalmente publicado en idioma inglés: Palopoli N., Marchetti J., Monzon A., Zea D., Tosatto S., Fornasari M., Parisi G., “Intrinsically Disordered Protein Ensembles Shape Evolutionary Rates Revealing Conformational Patterns”, Journal of Molecular Biology, Volume 433, Issue 3, 2021, 166751, ISSN 0022-2836, https://doi.org/10.1016/j.jmb.2020.166751.
Autores: Julia Marchetti*,1 Nicolas Palopoli*,1 Alexander M. Monzon,2 Diego J. Zea3, Silvio C. E. Tosatto2, Maria S. Fornasari1 y Gustavo Parisi1.
1 Departamento de Ciencia y Tecnología, Universidad Nacional de Quilmes, CONICET, Bernal, Buenos Aires, Argentina.
2 Department of Biomedical Sciences, University of Padua, Padua, Italia.
3 Sorbonne Université, CNRS, IBPS, Laboratoire de Biologie Computationnelle et Quantitative (LCQB), Paris, Francia.
* Estos autores contribuyeron en la misma extensión en la elaboración de este trabajo.
1En este trabajo se usa la palabra ensemble en inglés ya que es el término utilizado en la literatura del campo y, además, porque su traducción al español (conjunto o ensamble) no representa fidedignamente el concepto que se quiere ilustrar.
El estado nativo de las proteínas está compuesto por múltiples confórmeros que se encuentran en un equilibrio dinámico. En conjunto, todas estas estructuras forman lo que se conoce como ensemble nativo (Wei, Xi, Nussinov, Ma, 2016). Para el caso de proteínas globulares (conocidas como “ordenadas”) o dominios globulares, las barreras energéticas presentes para las transiciones entre los distintos confórmeros son relativamente altas, permitiendo de esta manera explorar, mediante distintos métodos y técnicas experimentales, conformaciones discretas y bien establecidas (Monzon, Rohr, Fornasari, Parisi, 2016).
En un extremo del continuo estructural del espacio conformacional de las proteínas, se pueden encontrar confórmeros que presentan pequeñas diferencias estructurales entre ellos (comportamiento típico de proteínas llamadas rígidas) donde movimientos pequeños o rotaciones en residuos que no involucran traslaciones a nivel del esqueleto carbonado permiten la llegada de ligandos al sitio activo de la proteína, la apertura de túneles, o el alargamiento de cavidades (Monzon et al., 2017). Los movimientos en loops, el desplazamiento de elementos de estructura secundaria y la rotación de dominios contribuyen al incremento de las diferencias estructurales entre confórmeros (Gerstein, Krebs, 1998).
En el otro extremo del continuo estructural se encuentran las IDPs, que presentan una alta plasticidad y barreras energéticas bajas entre los distintos confórmeros (Berlow, Dyson, Wright, 2015). Las características distintivas de este conjunto de proteínas no suponen una restricción para su distribución en los distintos reinos y taxas. Por ejemplo, aproximadamente el 40% de los proteomas de eucariotas (Lobanov, Galzitskaya, 2015) y aproximadamente el 46% de entradas de Uniprot (The UniProt Consortium, 2017) contienen regiones desordenadas cortas (Necci, Piovesan, Tosatto, 2016). Más aún es bien conocido el hecho que estas proteínas juegan un rol crucial en muchas enfermedades neurodegenerativas y en desórdenes sistémicos (Uversky et al., 2009).
Tanto para las proteínas globulares (u ordenadas) como para las IDPs, el concepto del ensemble estructural nativo es clave para dos explicaciones alternativas sobre la descripción de una serie de eventos complejos relacionados con la unión a ligando (Nussinov, Ma, Tsai, 2014 ). Estas dos explicaciones son el modelo de selección conformacional (de pre-equilibrio) y el modelo de encaje o ajuste inducido. Brevemente, en el modelo de selección conformacional un conjunto de conformaciones que se encuentran pobremente representadas puede presentar una alta afinidad para un determinado ligando biológico. Los eventos de unión producen un cambio en el equilibrio conformacional que produce un incremento en la concentración relativa de estas conformaciones competentes, fenómeno denominado population shift. Por otro lado, el modelo de ajuste inducido propone que la adopción de una conformación preferida ocurre luego del evento de unión al ligando, en un proceso que puede involucrar, en el caso de IDPs, cambios conformacionales y transiciones orden-desorden. Cualquiera sea el modelo apropiado para explicar la biología de una proteína determinada (Hammes, Chang, Oas, 2009), la pre-existencia de conformaciones escasamente pobladas competentes o la reestructuración conformacional posterior a la unión de ligando, trae aparejada la noción que las IDPs no son proteínas completamente desestructuradas (Berlow et al., 2015) y que existen determinadas conformaciones que contienen información estructural residual que juega un papel clave en la función biológica de dicha proteína (Berlow et al., 2015; Davey, 2019; Reisen, Weisel, Kriegl, Schneider, 2010; Mészáros et al., 2019; Zea et al., 2016).
Un parámetro que es extensamente utilizado para predecir las velocidades de evolución es el nivel de expresión génica (Drummond, Bloom, Adami, Wilke, Arnold, 2005 ) encontrándose una relación inversa, entendiendo a las velocidades de evolución de las proteínas como un parámetro global. Sin embargo, cada posición de cada proteína puede evolucionar bajo una presión de selección distinta del resto de las posiciones y dar origen a velocidades de evolución heterogéneas en una misma proteína. Por ejemplo, para las proteínas ordenadas, los sitios que presentan un gran número de contactos entre residuos, o con una alta densidad de empaquetamiento (como aquellos residuos que forman parte del núcleo proteico), o con baja exposición al solvente, tienden a evolucionar más lento (Yeh et al., 2014; Franzosa, Xia, 2009; Tóth-Petróczy, Tawfik, 2011). Muchos estudios encontraron correlaciones entre velocidades de evolución sitio-específicas y distintas características estructurales (para un recuento, véase Echave, Spielman, Wilke, 2016).
¿Qué sucede con las IDPs y con las Regiones Intrínsecamente Desordenadas (Intrinsically Disordered Regions, IDRs)? Es preciso tener presente que el universo proteico es mucho más amplio y no solamente comprende proteínas globulares. En una primera aproximación, las regiones desordenadas tienden a evolucionar más rápido que las proteínas ordenadas (Brown et al., 2002). Esto es un resultado esperable debido a que sus residuos presentan un bajo número de contactos entre ellos (Dosztányi, Csizmók, Tompa, Simon, 2005) y una alta exposición al solvente (Davey, 2019). A pesar que trabajos previos detectaron sitios restringidos evolutivamente en IDPs (Toth-Petroczy et al., 2016; Marchetti, Monzon, Tosatto, Parisi, Fornasari, 2019; Pancsa, Zsolyomi, Tompa, 2018), el rol que estos sitios tienen en las IDPs con una alta flexibilidad estructural no está claro. En proteínas que poseen una alta diversidad conformacional (como es el caso de las IDPs), podría esperarse que algunos confórmeros que se encuentran parcialmente plegados y que presentan elementos de estructura secundaria transitorios impongan condicionamientos estructurales específicos y aditivos sobre las velocidades de evolución sitio-específicas. En este trabajo se describen las metodologías y resultados para respaldar esta última hipótesis mediante la evaluación del impacto que tiene la información estructural de IDPs derivada de datos experimentales en la velocidad de evolución. Incluso podría suceder que estos condicionamientos estructurales derivados del ensemble nativo revelen la existencia de distintos tipos de funcionalidad de IDPs, en especial aquellas relacionadas con transiciones orden-desorden posterior a la unión a ligando (Davey, 2019).
El conjunto de datos utilizado en este trabajo consistió en 310 estructuras de IDPs obtenidas por NMR. Estas proteínas contienen al menos el 40% de sus posiciones desordenadas (para una explicación más detallada sobre la estimación de desorden, véase la sección “Métodos”). La Figura 1 ilustra una estructura típica de una IDP distinguiendo entre regiones ordenadas (en color azul) y desordenadas (rojo). De la comparación entre las velocidades de evolución normalizadas de ambos tipos de regiones, presentes en todo el conjunto de datos, se puede deducir que las regiones desordenadas de las IDPs tienen tasas de evolución significativamente más altas que las regiones ordenadas de las mismas proteínas (Figura 2).

Figura 1: Representación de unensemble IDPs. Ambas figuras son una representación hecha con el software PyMol de la misma proteína promotora de polimerización de tubulina de humanos (TPPP3 código PDB: 2JRF). En la figura de la izquierda se resaltan en color rojo las posiciones desordenadas mientras que en el lado derecho de la figura se muestran las posiciones ordenadas en color azul.
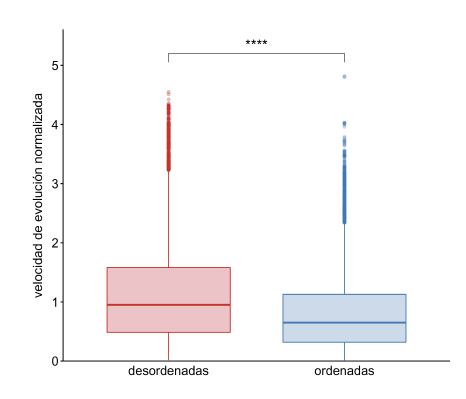
Figura 2: Diagrama de cajas representando la distribución de las velocidades de evolución normalizadas por posición. Dentro del conjunto de datos entero de IDPs, las velocidades normalizadas para las posiciones desordenadas se muestran en color rojo (mediana de 0.95) y las posiciones ordenadas en azul (mediana de 0.65). Para las comparaciones estadísticas se realizó un test de Wilcoxon, los asteriscos representan valores de distinta significancia: ****, valores-p <= 0.0001; ***, valores-p <= 0.001; **, valores-p <= 0.01; *, valor-p <= 0.05; y la expresión “ns” (no significativo) implica que se obtuvo un valor-p > 0.05.
Esta heterogeneidad observada en las velocidades de evolución de IDPs se comprende mejor si se estudia cuál es la relación de los perfiles de velocidades posición-específica con la variación estructural observada en el ensemble proteico. Se observa que las velocidades de evolución por sitio muestran una alta correlación con su variación estructural en el ensemble, medida con el parámetro RMSF (Root Mean Square Fluctuation) de sus carbonos alfa como se muestra en la Figura 3. Cada panel de la figura colecta proteínas que presentan un arreglo estructural de desorden determinado (para más información sobre las proteínas utilizadas, véase la descripción y los paneles de la derecha de la Figura 3) y que por lo tanto presentan perfiles de velocidad de evolución similares (véase Figura 3, panel izquierdo) así como también perfiles de RMSF similares (véase Figura 3, panel central). Cabe destacar que las proteínas representadas en cada panel no son homólogas entre sí: son proteínas funcional y secuencialmente alejadas que, sin embargo, poseen la misma organización estructural en cuanto al patrón de orden-desorden.
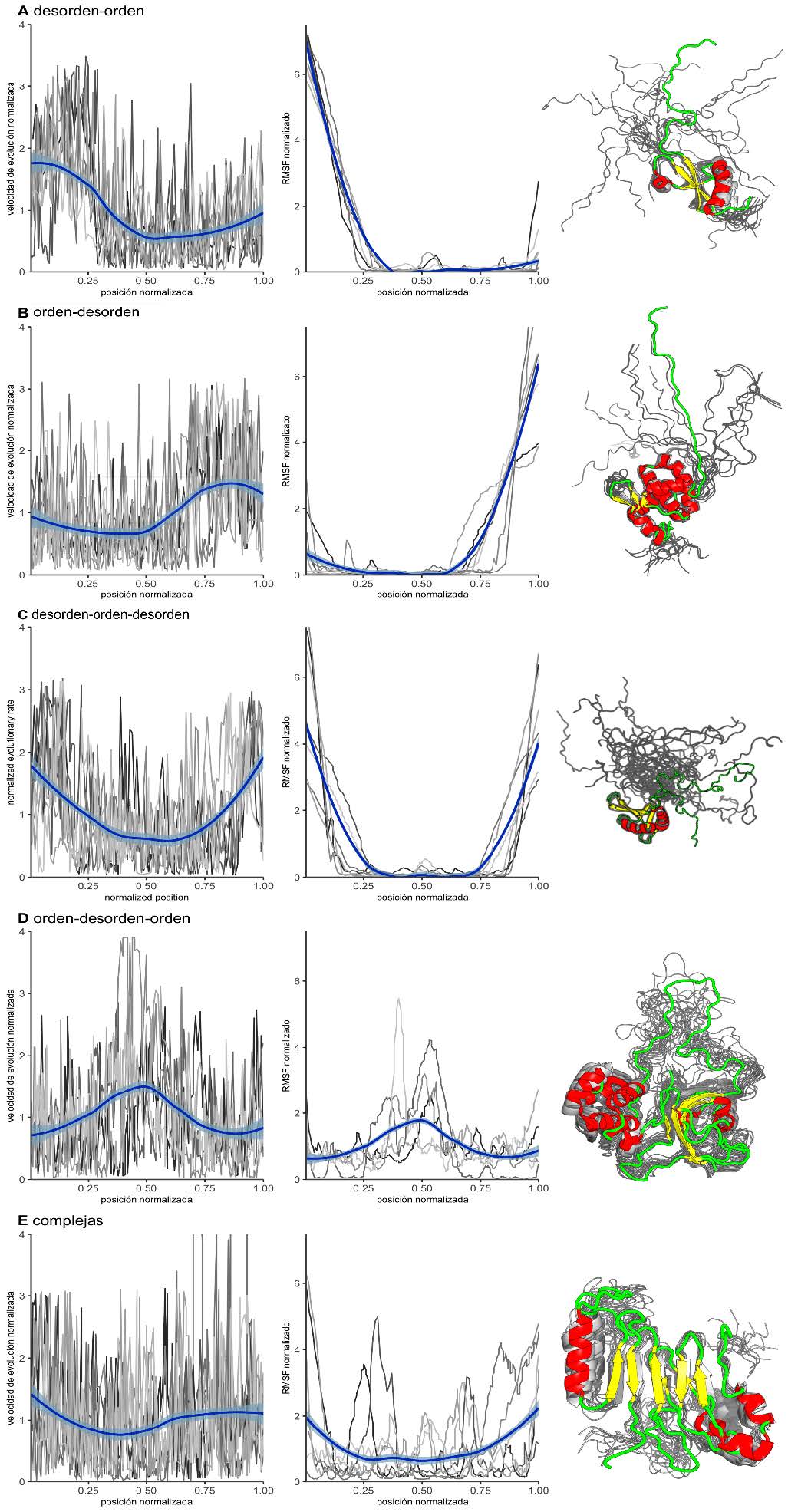
Figura 3: Perfiles de velocidad normalizada y de RMSF. A la izquierda se grafican perfiles de velocidad de evolución normalizada; en el centro, perfiles del RMSF normalizados; a la derecha, proteína representativa de cada uno de los arreglos estructurales encontrados. En color azul se destacan las curvas obtenidas por regresión LOESS. Los perfiles en gris corresponden a las cadenas proteicas para cada grupo y, debajo, los códigos PDB. Marcadas con asteriscos están las proteínas utilizadas para la representación esquemática que se muestra a la derecha de cada panel. Panel A: proteínas que presentan un arreglo estructural del tipo desorden-orden (PDBids: 2cqrA, 2k3aA, 2khmA, 2myxA, 2rsmA, 2rsoA, *2rvlA). Panel B: proteínas que presentan un arreglo estructural del tipo orden-desorden (PDBids: 1uffA, 1ug1A, 1jvrA, *2hmxA, 2k4kA, 2k5fA, 2ru8A). Panel C: proteínas que presentan un arreglo estructural del tipo desorden-orden-desorden (PDBids: 1ixdA, *1u6fA, 1wj7A, 2dh7A, 2ecbA, 2ejmA, 2k8pA). Panel D: proteínas que presentan un arreglo estructural del tipo orden-desorden-orden (PDBids: 1qu6A, 2adzA, 2lbcA, 2l3sA, *2mphA). Panel E: proteínas que presentan un arreglo estructural complejo (PDBids: 1mm4A, 1sm7A, 1tteA, 1vzsA, *2aivA, 2afjA, 2n1rA).
Si se observa el panel de la derecha de la Figura 3, se pueden ver representaciones esquemáticas de proteínas con determinados arreglos estructurales. Es importante destacar que las regiones desordenadas pueden encontrarse en distintas partes de las proteínas: en la parte central o en los extremos (entiéndase por extremos amino o carboxilo terminal los correspondientes a la proteína o bien a los límites entre dominios, ya que un tercio de los polipéptidos presentes en el conjunto de datos son dominios que se encuentran presentes en la estructura de al menos 30 residuos de los extremos de la proteína). Estos perfiles de velocidad de evolución pueden ser utilizados para distinguir como mínimo cinco tipos distintos de organizaciones estructurales en proteínas:
- 1)
Proteínas que contienen una región N-terminal desordenada seguida de una región globular (panel A de la Figura 3). Como representante de este grupo se tomó al dominio N-terminal de la heterocromatina 1 de murino (Shimojo et al., 2016) (código PDB: 2RVL). El extremo N-terminal de esta proteína es polianfolítico y su flexibilidad es regulada por la fosforilación de sus serinas, lo que altera la distribución del ensemble conformacional, desplazándolo hacia aquellos confórmeros donde hay unión con la histona H3. Si se observa el lado izquierdo del panel A, se verá que las velocidades de evolución son más altas en la región de alta flexibilidad, que en este caso se corresponde con el extremo amino terminal.
- 2)
Proteínas que contienen una región N-terminal ordenada seguida de una región desordenada (panel B de la Figura 3). En este caso se tomó como representante para la esquematización el dominio alfa-hélice del precursor de la poliproteína Gag del HIV-1 (código PDB: 2HMX). En esta poliproteína, la región desordenada une MA al dominio N- terminal de la proteína CA. Recientemente se sugirió que la contracción de ese conector (linker) desordenado puede permitir la interacción entre la MA (inmadura) y el dominio CA, regulando la accesibilidad de la proteasa viral para la liberación de proteínas maduras (Samsudin, Gan, Bond, 2020). Al igual que el grupo anterior, estas proteínas presentan velocidades de evolución más altas en su extremo flexible, que en este caso es el extremo carboxilo terminal.
- 3)
Proteínas que presentan una organización estructural con una alternancia desorden-orden-desorden (panel C de la Figura 3). En este caso se tomó como representante a la proteína UBI-1 del parásito Trypanosoma cruzi. La proteína contiene un motivo de reconocimiento de RNA flanqueado por regiones N-terminal y C-terminal desordenadas (código PDB: 1U6F) (Volpon, D’Orso, Young, Frasch, Gehring, 2005). La región ordenada es evidenciada por una disminución concomitante tanto en el perfil de velocidad como en el de flexibilidad.
- 4)
Proteínas que presentan una organización estructural con una alternancia orden-desorden-orden (panel D de la Figura 3). Como representante de este grupo se tomó a la inmunofilina nuclear FKBP25 (código PDB: 2MPH). Esta proteína presenta un dominio N-terminal HLH y un dominio C-terminal de unión a FK506 que se encuentran unidos por un conector largo y flexible que permite el correcto reconocimiento del ADN por cualquiera de los dos dominios globulares (Prakash, Shin, Rajan, Yoon, 2016).
- 5)
Proteínas que presentan una organización estructural de desorden complejo (panel E de la Figura 3). Estas proteínas se caracterizan por tener regiones desordenadas cortas, embebidas en dominios globulares o formando parte de regiones de transición orden-desorden. Como ejemplo, se muestra una representación de la proteína del poro nuclear de levaduras NUP116P (código PDB: 2AIV) (Robinson et al., 2005) que presenta regiones con estructura secundaria bien definida intercaladas con loops flexibles.
Efectos de los contactos entre residuos en las velocidades de evolución
Se ha establecido que la estructura de la proteína tiene un gran impacto en las velocidades de evolución (Echave, Spielman, Wilke, 2016). Las velocidades de evolución en posiciones ordenadas y desordenadas podrían estar condicionadas o podrían ser explicadas si se consideran el número de contactos entre residuos. El promedio de contactos por posición en posiciones ordenadas es de 3.44, mientras que para las posiciones desordenadas es de 1.75. Es decir, en promedio las posiciones ordenadas tienen el doble de contactos físicos que las posiciones desordenadas. Como se puede observar en la Figura 2, las posiciones desordenadas de las IDPs presentan tasas de evolución más altas pero, también, algunas pueden evolucionar tan lento como posiciones ordenadas. Entonces, ¿cómo es posible que a pesar de tener en promedio menor cantidad de contactos terciarios, las posiciones desordenadas puedan presentar tasas evolutivas comparables con las de posiciones ordenadas? Los ensembles de IDPs están formados por conformaciones que presentan una alta tasa de interconversión y que además son estructuralmente muy diferentes entre sí, por lo que la cantidad de contactos entre residuos para una determinada posición puede cambiar sustancialmente entre distintas conformaciones. Entonces, fue necesario derivar alguna métrica estructural que diera cuenta de la información presente en todo el ensemble. Una de esas métricas es el promedio de contactos por posición, que se calculó de la siguiente manera (Figura 4).
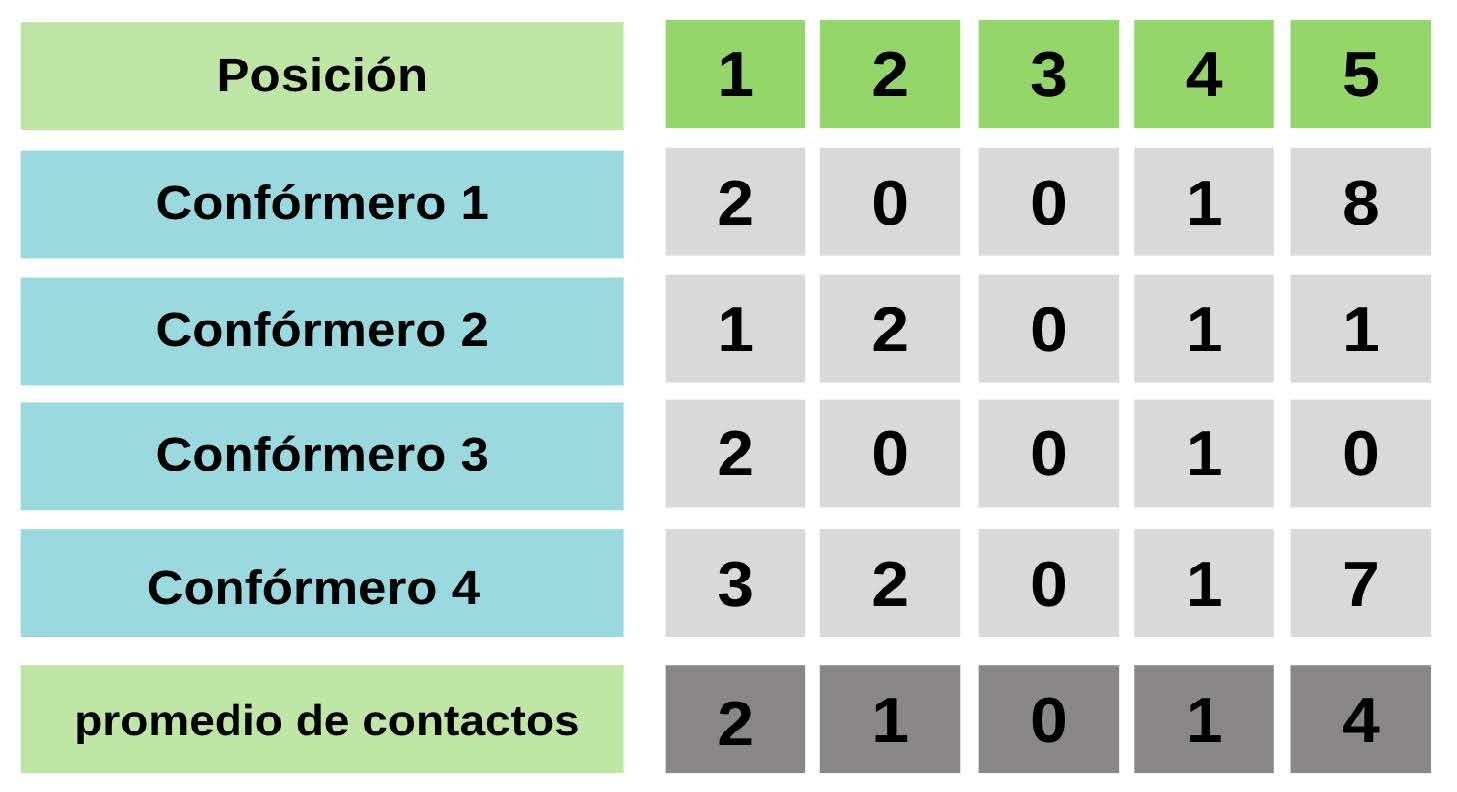
Figura 4: Esquema de cálculo del promedio de contactos a lo largo del ensemble El promedio de contactos se calcula simplemente promediando la cantidad de contactos observados para una determinada posición a lo largo del ensemble.
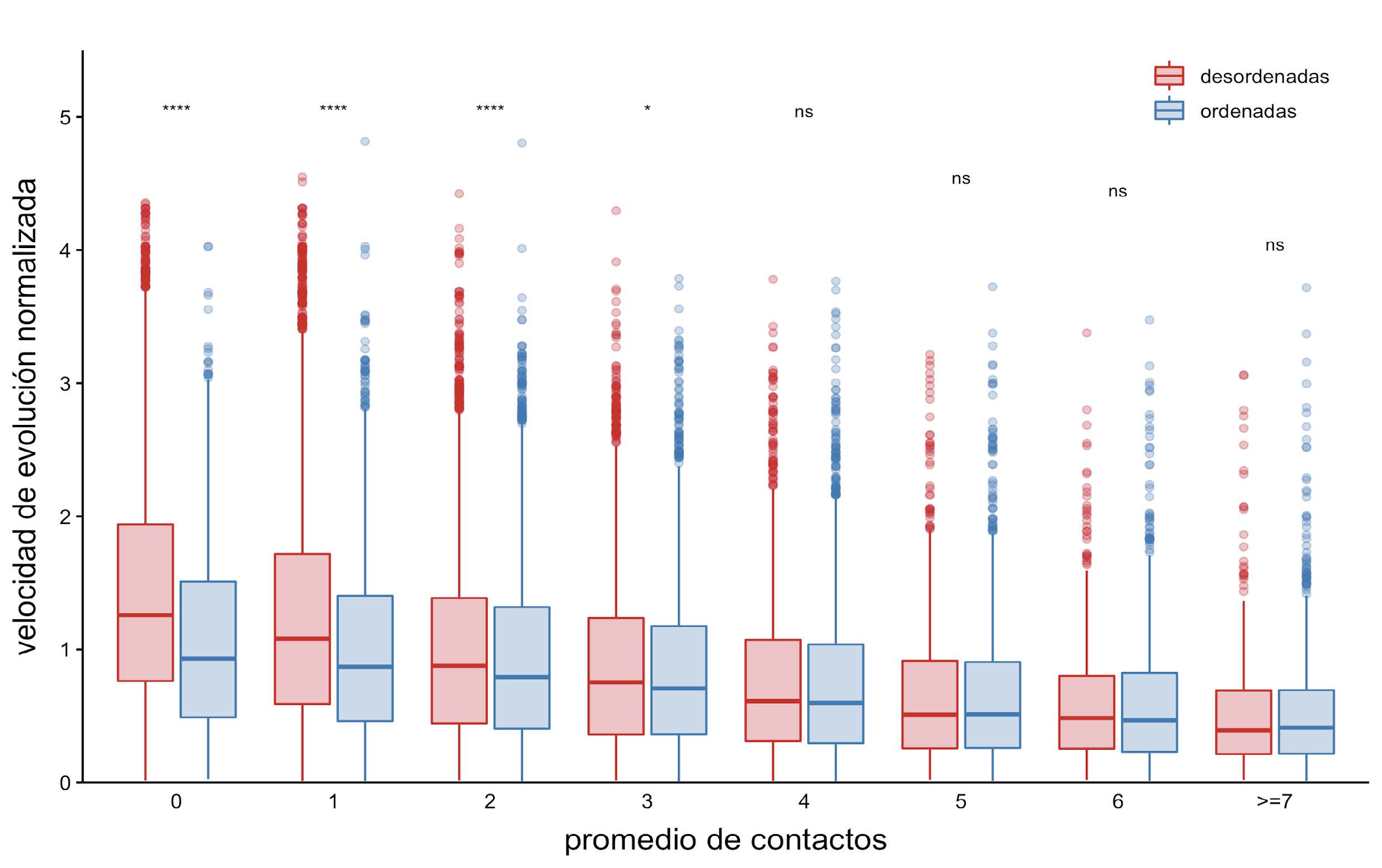
Figura 5: Velocidad de evolución normalizada en función del promedio de contactos
Los diagramas de caja muestran la distribución de la velocidad normalizada en función del promedio de contactos por posición a lo largo de todo el ensemble. Para las comparaciones estadísticas se realizó un test de Wilcoxon, los asteriscos representan: ****, valores-p <= 0.0001; ***, valores-p <= 0.001; **, valores-p <= 0.01; *, valor-p <= 0.05; y la expresión “ns” (no significativo) implica que se obtuvo un valor-p > 0.05.
Si se considera el promedio de número de contactos por posición a lo largo de todo el ensemble, se puede observar una tendencia negativa entre la velocidad de evolución normalizada y el promedio de contactos, independientemente si esa posición es ordenada o desordenada (Figura 5). También, es interesante notar que las posiciones ordenadas y las desordenadas tienden a presentar tasas de evolución similares cuando el número de contactos aumenta. Este mismo resultado se obtiene cuando se compara con el máximo, el mínimo y la moda en el número de contactos derivados de todo el ensemble (Figura 6).

Figura 6: Velocidad de evolución normalizada en función de información de contactos. Los diagramas de caja muestran las distribuciones de las velocidades de evolución normalizadas en función de distintas métricas estructurales. Cada una de estas métricas son derivadas del ensemble, como el máximo, el mínimo y la moda de contactos para una determinada posición a lo largo del ensemble. Para las comparaciones estadísticas se realizó un test de Wilcoxon, los asteriscos representan valores de distinta significancia: ****, valores-p <= 0.0001; ***, valores-p <= 0.001; **, valores-p <= 0.01; * , valor-p <= 0.05; y la expresión “ns” (no significativo) implica que se obtuvo un valor-p > 0.05.
Otra métrica estructural utilizada para caracterizar el comportamiento dinámico de las IDPs es el parámetro que se denomina “robustez” de contactos, que contabiliza la fracción de confórmeros con al menos un contacto por sitio. Entonces, una robustez o fracción de contactos del 50% significa que para esa posición la mitad de los confórmeros del ensemble están haciendo contacto. Para esta determinación no importa si esa posición realiza 4 contactos con otro residuo o 1, es contabilizada como una posición con al menos un contacto. El esquema del cálculo de dicha fracción se ilustra en la Figura 7.
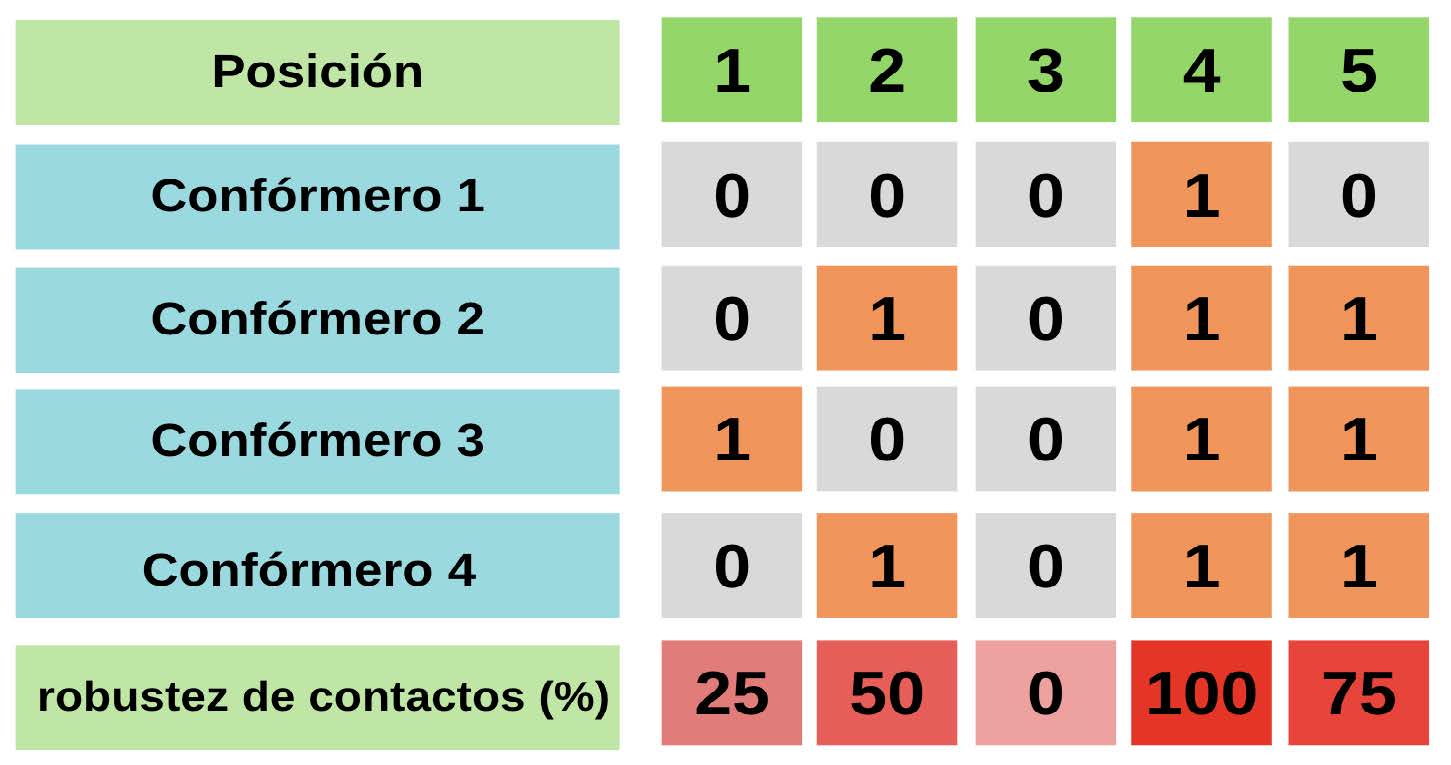
Figura 7: Esquema de cálculo de robustez de contacto para un ensemble. Para el esquema se ejemplifica con un ensemble de 4 confórmeros. La robustez de contactos se expresa en porcentaje, pero en fracción es análoga. Es decir, una robustez de 0.5 equivale a una robustez del 50% y viceversa. Si una posición no establece ningún contacto con otros residuos, se le asigna un 0. Si una posición establece un contacto o más con otra posición, se le asigna un 1. La robustez de contactos se calcula contando para qué fracción del ensemble entero esa posición establece contacto. Por ejemplo, en el esquema, la posición 1 presenta solamente contactos en el confórmero 3, entonces la fracción de contactos se calcula como 1 dividido el total de confórmeros en el ensemble, que son 4, lo que arroja una robustez del 25%. Por otro lado, la posición 5 presenta contacto en el confórmero 2, 3 y el 4, dando lugar a una robustez del 75%.
Además, la fracción de contactos puede ser interpretada como la robustez que tiene esa posición para mantener al menos un contacto a lo largo del ensemble. Una posición que tiene contactos en el 70% de los confórmeros es más robusta que una posición que solamente la tiene en el 10%, y por eso se definió a esa fracción como robustez de contacto. Como era esperable, las posiciones desordenadas tienen en promedio valores más bajos de robustez de contactos (~0.67) que las posiciones ordenadas (~0.92). Esto significa que las posiciones ordenadas tienden a mantener los contactos a lo largo de todo el ensemble (Figura 8).
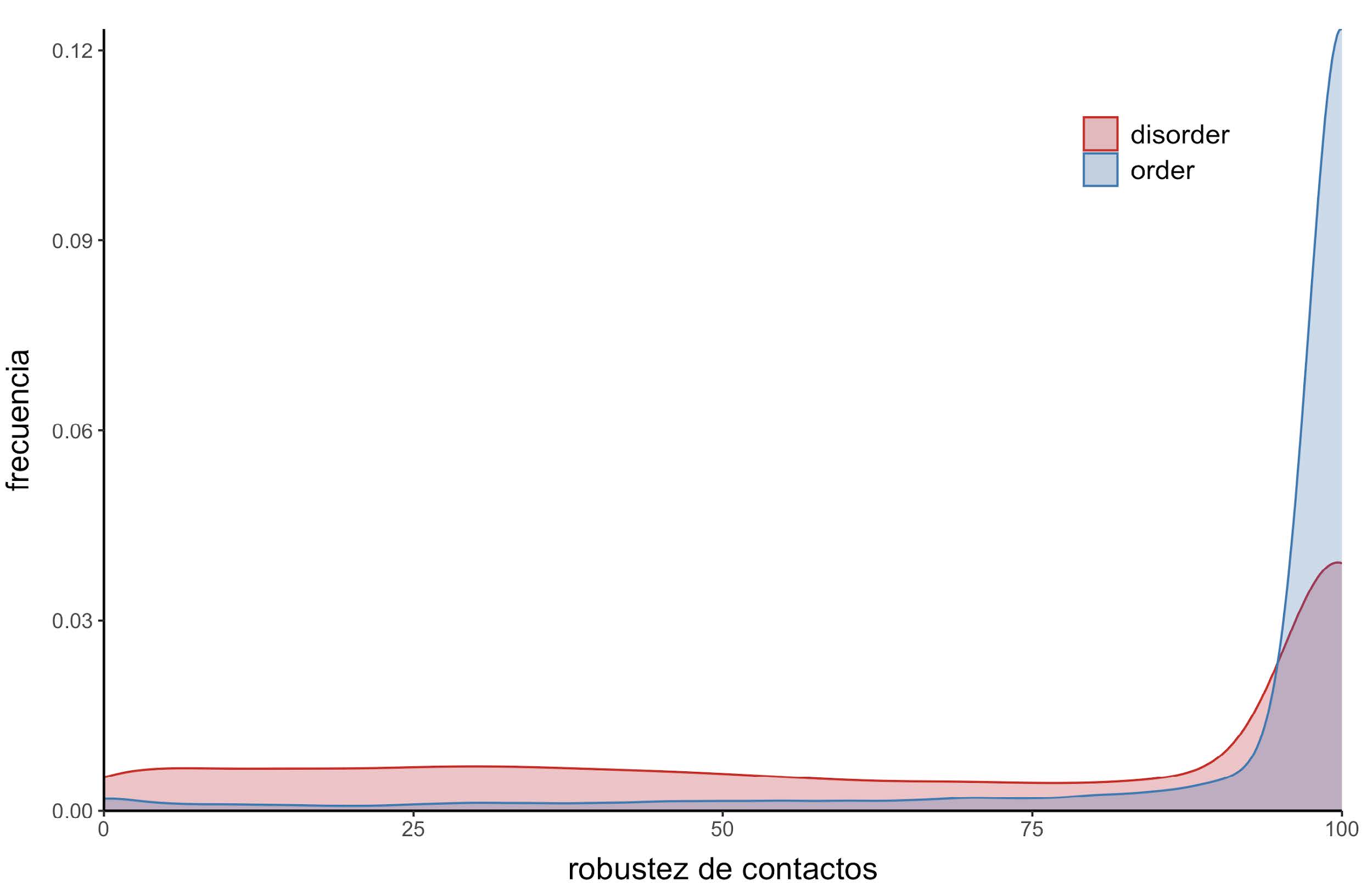
Figura 8: Distribución de la robustez de contactos. Las posiciones desordenadas se ilustran en color rojo y las ordenadas en azul.
Que las posiciones ordenadas tengan en promedio mayor robustez de contacto que las desordenadas era esperable debido a su naturaleza y al rol que tienen en el mantenimiento de una estructura tridimensional determinada, establecida principalmente por contactos terciarios entre residuos. Como puede verse en la Figura 8, existen posiciones desordenadas que también presentan valores altos de robustez, e incluso alrededor del 40% de ellas presenta un valor del 100%. Evidentemente, el mantenimiento de contactos en determinadas posiciones resulta importante a pesar de que una posición esté predicha como desordenada, ya que esa predicción no implica necesariamente una pérdida de características estructurales. El desorden es un elemento estructural y debe ser tenido en cuenta para entender el rol biológico de las IDPs.
Entonces, ¿cuál es la relación entre la velocidad de evolución y la fracción o robustez de contactos para las posiciones desordenadas? En una primera aproximación, la robustez de contactos puede entenderse como determinante si es que toma el valor 0 (ningún confórmero tiene contactos en esa posición) o el valor 100 (todos los confórmeros mantienen al menos un contacto en esa posición). Si se observa la Figura 9, se puede concluir que la necesidad de mantener al menos un contacto en el 100% de las conformaciones restringe la velocidad de evolución para esa posición. El desorden es también un elemento estructural que modula la divergencia secuencial.
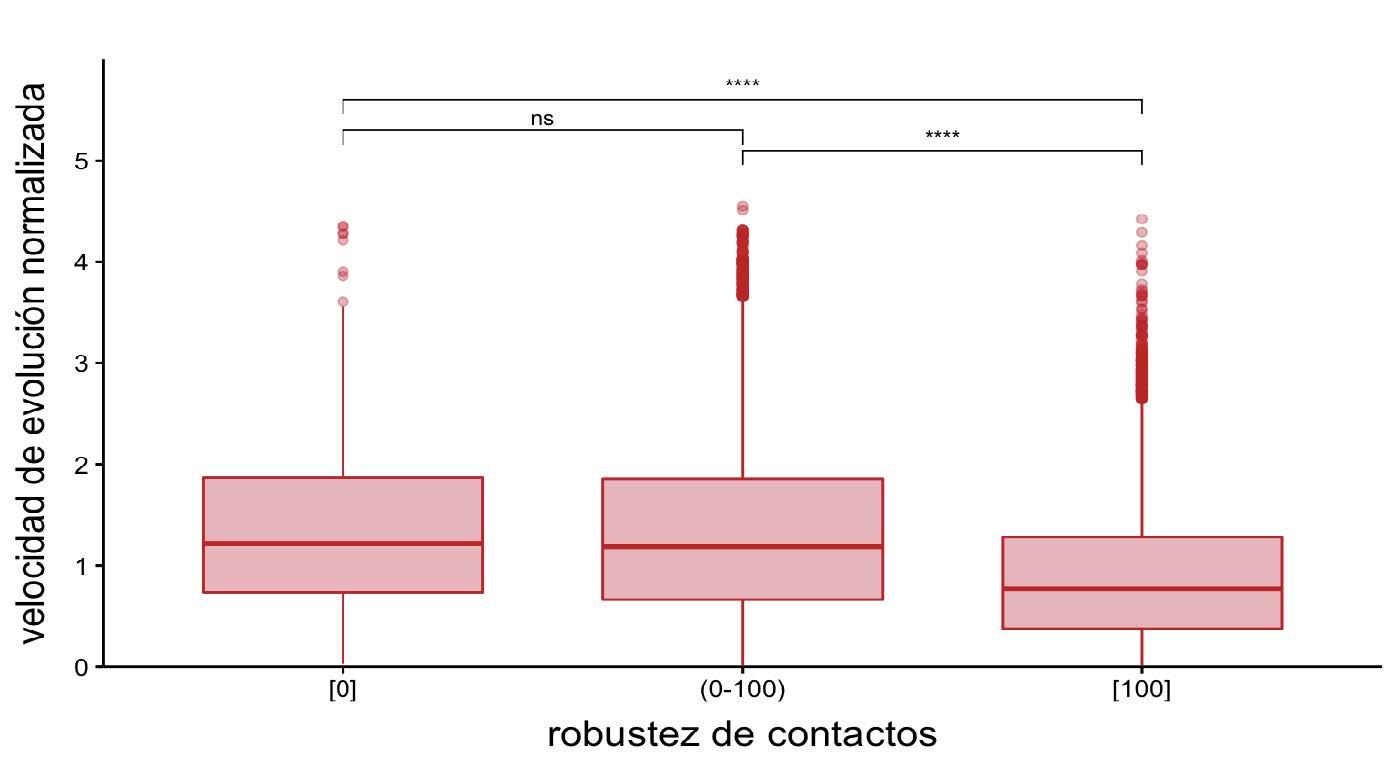
Figura 9: Distribución de las velocidades de evolución normalizadas en función de la robustez de contactos. En esta figura se resalta la relación entre las velocidades normalizadas de evolución para posiciones desordenadas con robustez nula (0 %) o completa (100 %) o algún valor dentro del intervalo (0-100). Para las comparaciones estadísticas se realizó un test de Wilcoxon, los asteriscos representan: ****, valores-p <= 0.0001; ***, valores-p <= 0.001; **, valores-p <= 0.01; *,valor-p <= 0.05; y la expresión “ns” (no significativo) implica que se obtuvo un valor-p > 0.05.
Si ahora se analiza el continuo de robustez en las posiciones desordenadas en función de las velocidades normalizadas de evolución puede observarse una tendencia similar al promedio de contactos: la velocidad de evolución se vuelve más lenta a medida que se incrementa la robustez de contactos (véase la Figura 10). Esto sugiere que la presencia del desorden podría ayudar a aumentar las velocidades de evolución en esas posiciones.
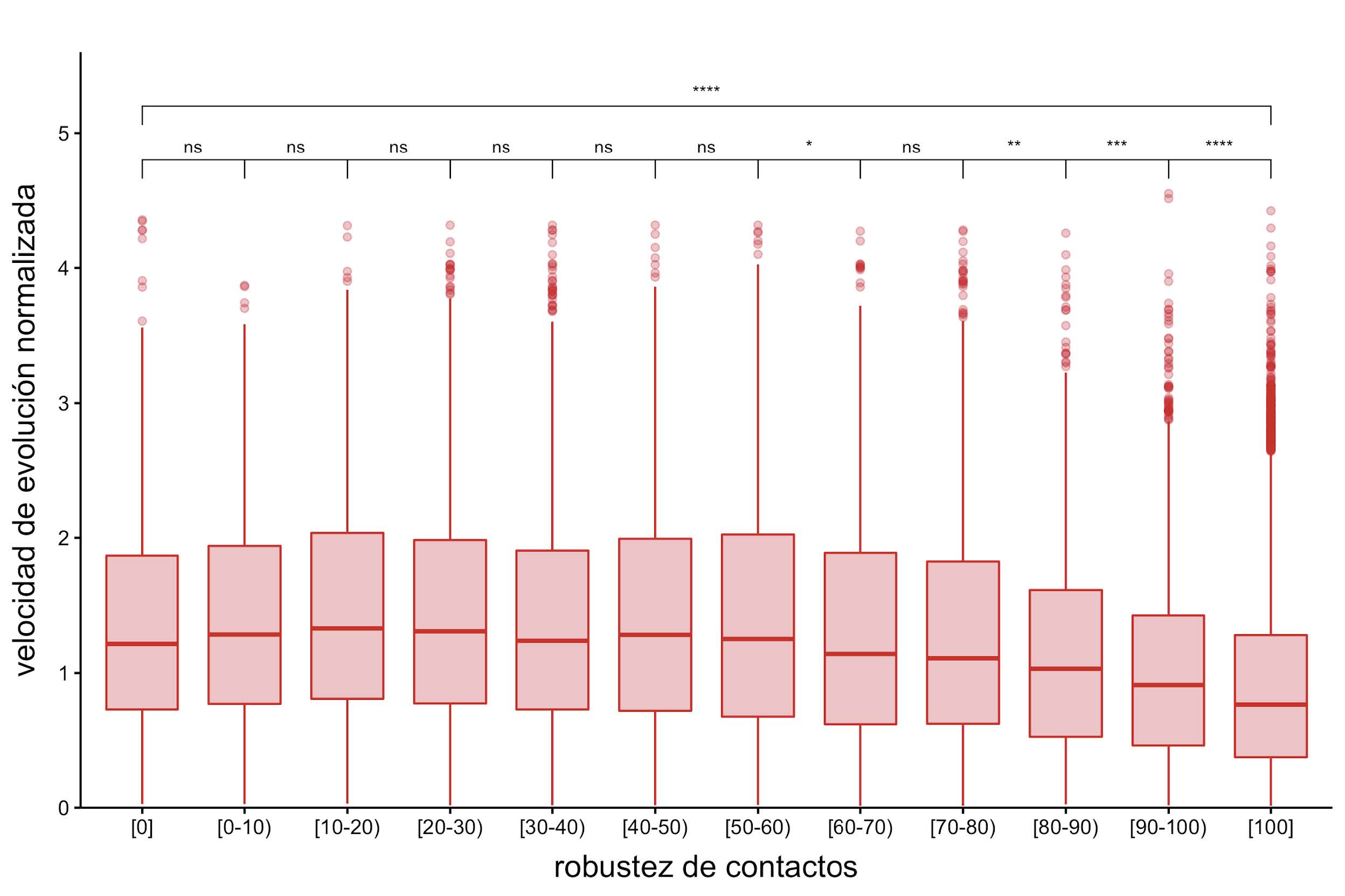
Figura 10: Velocidad de evolución normalizada en función de la robustez de contacto. En esta figura se resalta la relación entre las velocidades normalizadas de evolución para posiciones desordenadas y la robustez de contactos (expresada en porcentaje) clasificadas en intervalos más pequeños. Para las comparaciones estadísticas se realizó un test de Wilcoxon, los asteriscos representan valores de distinta significancia: ****, valores-p <= 0.0001; ***, valores-p <= 0.001; **, valores-p <= 0.01; *, valor-p <= 0.05; y la expresión “ns” (no significativo) implica que se obtuvo un valor-p > 0.05.
Como ya se ha mencionado, las IDPs son altamente dinámicas. Entonces, es posible pensar que otro de los factores que puede llegar a modular la velocidad de evolución en residuos desordenados es su interacción con regiones desordenadas y regiones ordenadas. Para probarlo, se estudia cómo es la velocidad normalizada de evolución, el promedio de los contactos por sitio, y los valores de RMSF normalizados en posiciones desordenadas en función a la distancia al residuo ordenado más cercano. Se observa que la velocidad de evolución normalizada aumenta a medida que lo hace la distancia al residuo ordenado más cercano (Figura 11). Una tendencia similar se observa entre el RMSF normalizado, que es un indicador del grado de flexibilidad en esa posición (Figura 12).
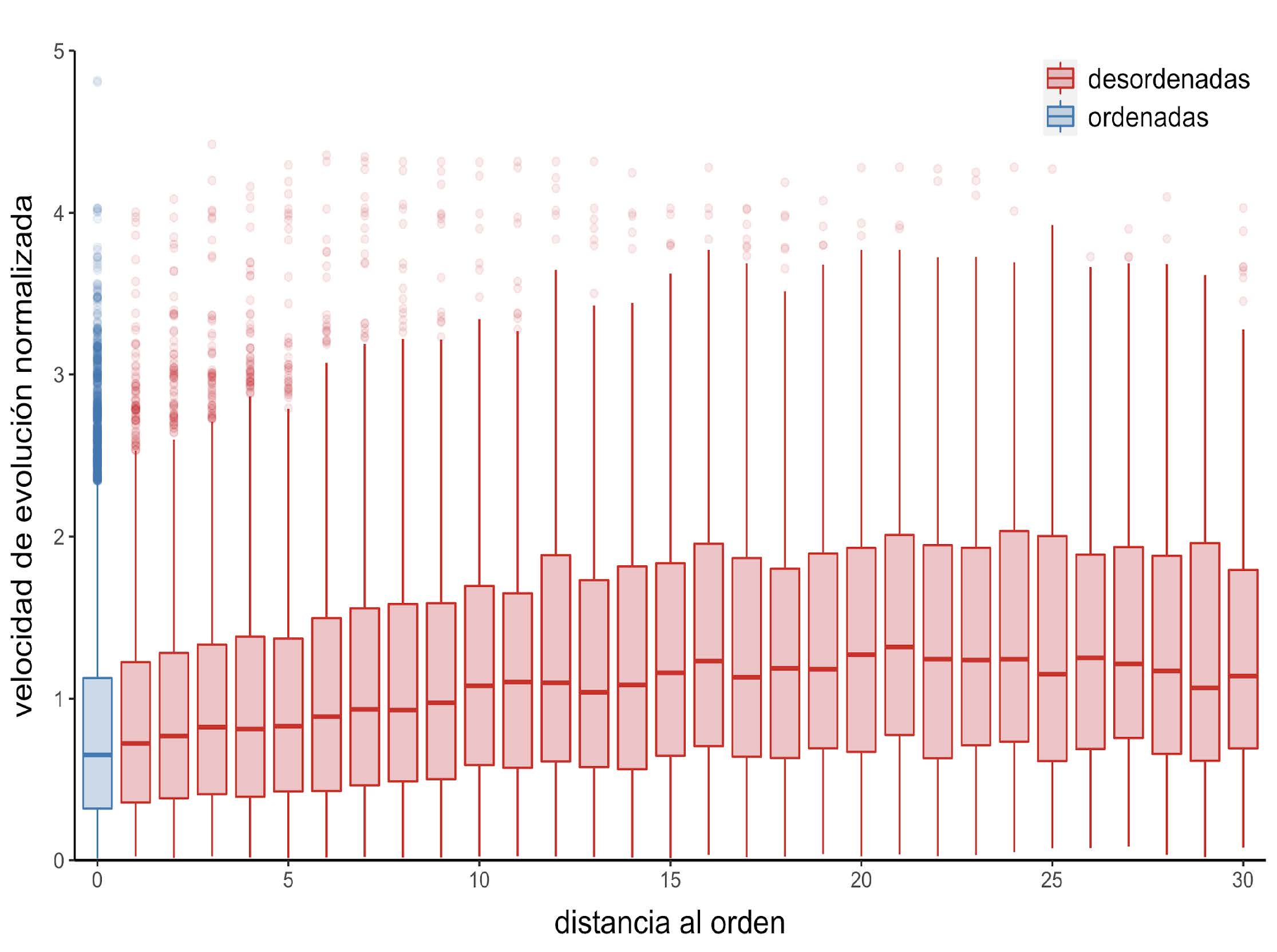
Figura 11: Distribución de las velocidades de evolución normalizadas en función de la distancia al residuo ordenado más cercano
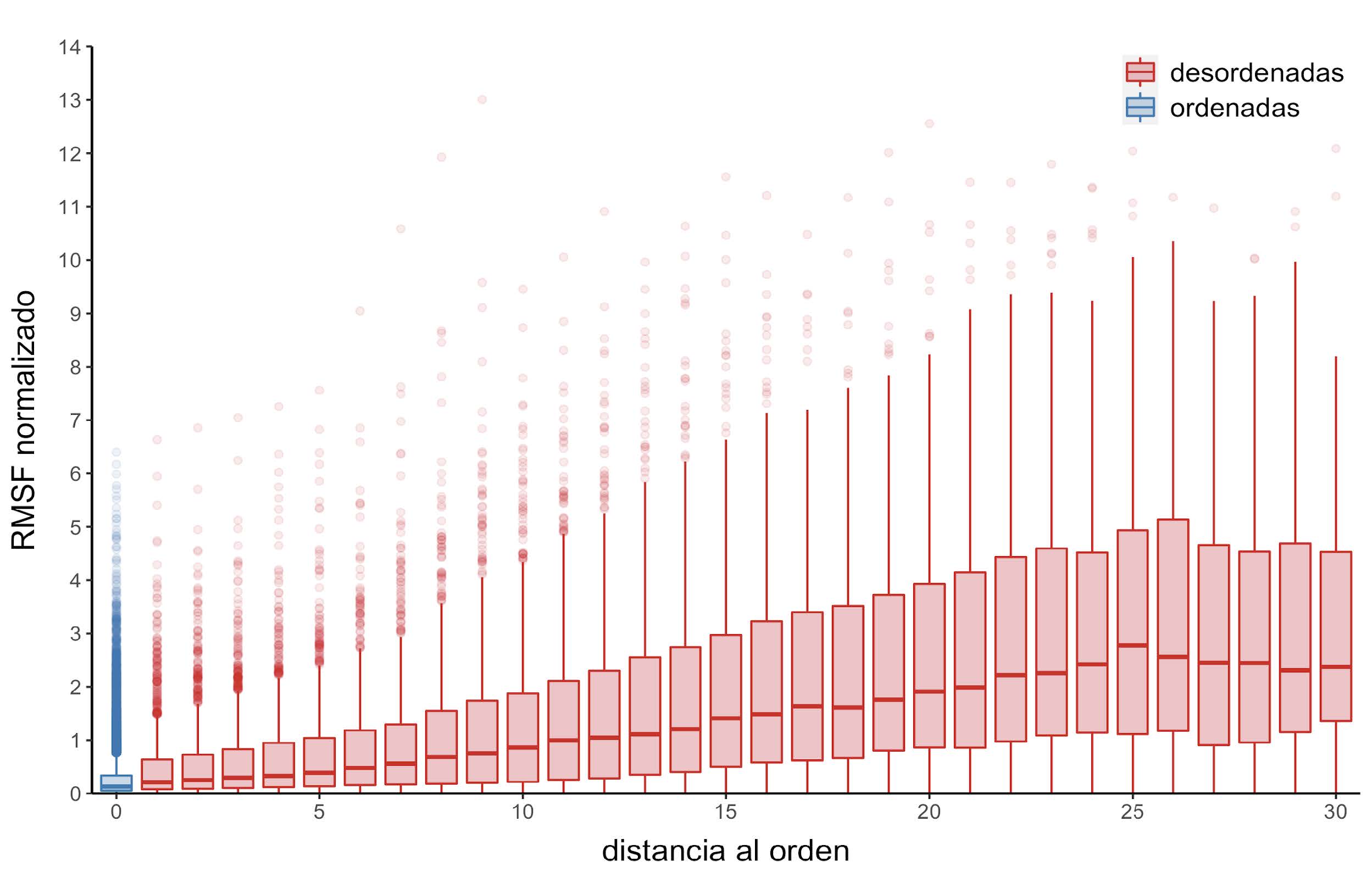
Figura 12: Distribución de RMSF normalizados en función de la distancia al residuo ordenado más cercano
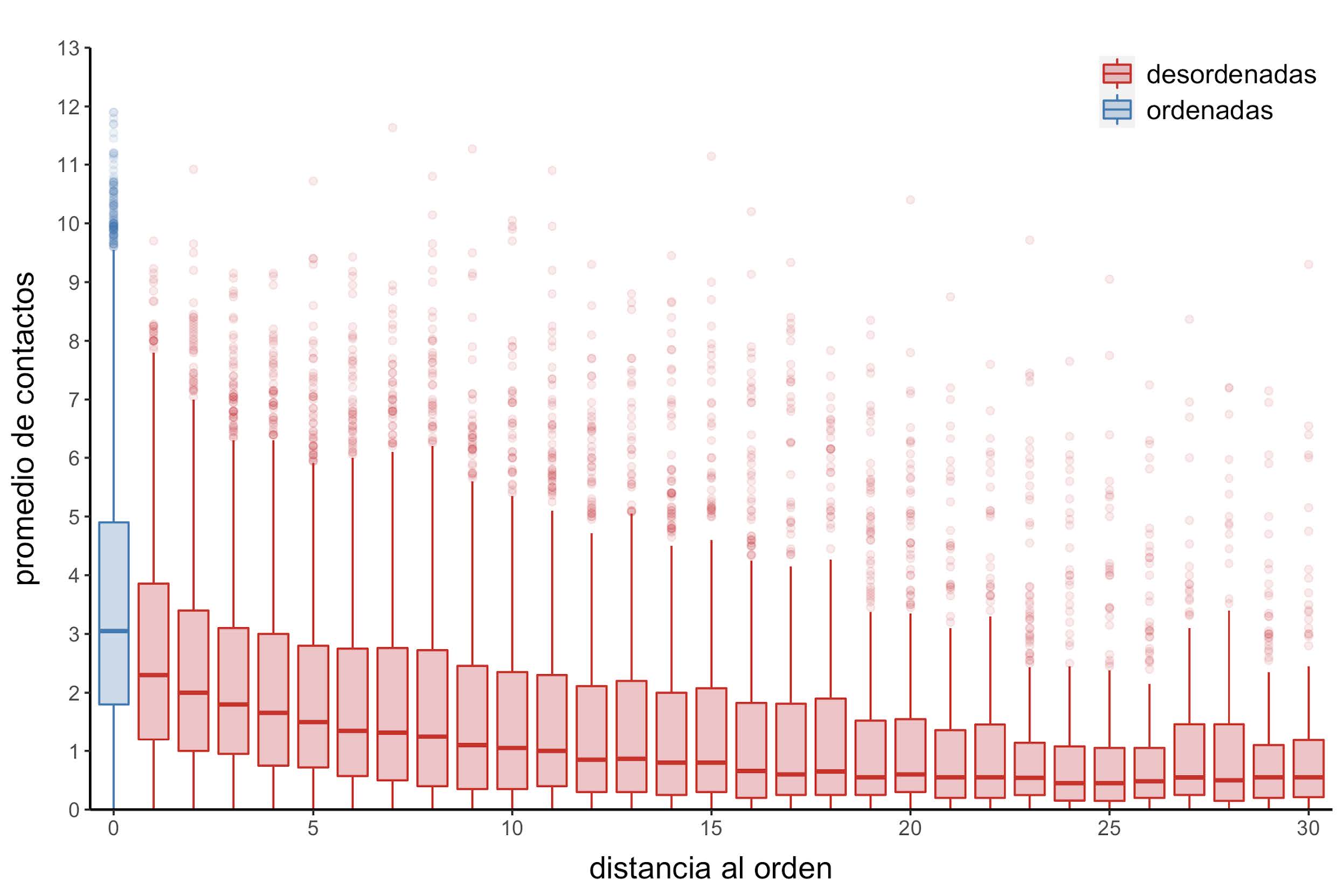
Figura 13: Distribución del promedio de contactos en función de la distancia al residuo ordenado más cercano
Mientras que el promedio de contactos disminuye a medida que aumenta la distancia al orden (Figura 13), este último resultado a su vez está acompañado con un incremento en la proporción de contactos establecidos entre regiones desordenadas (Figura 14).
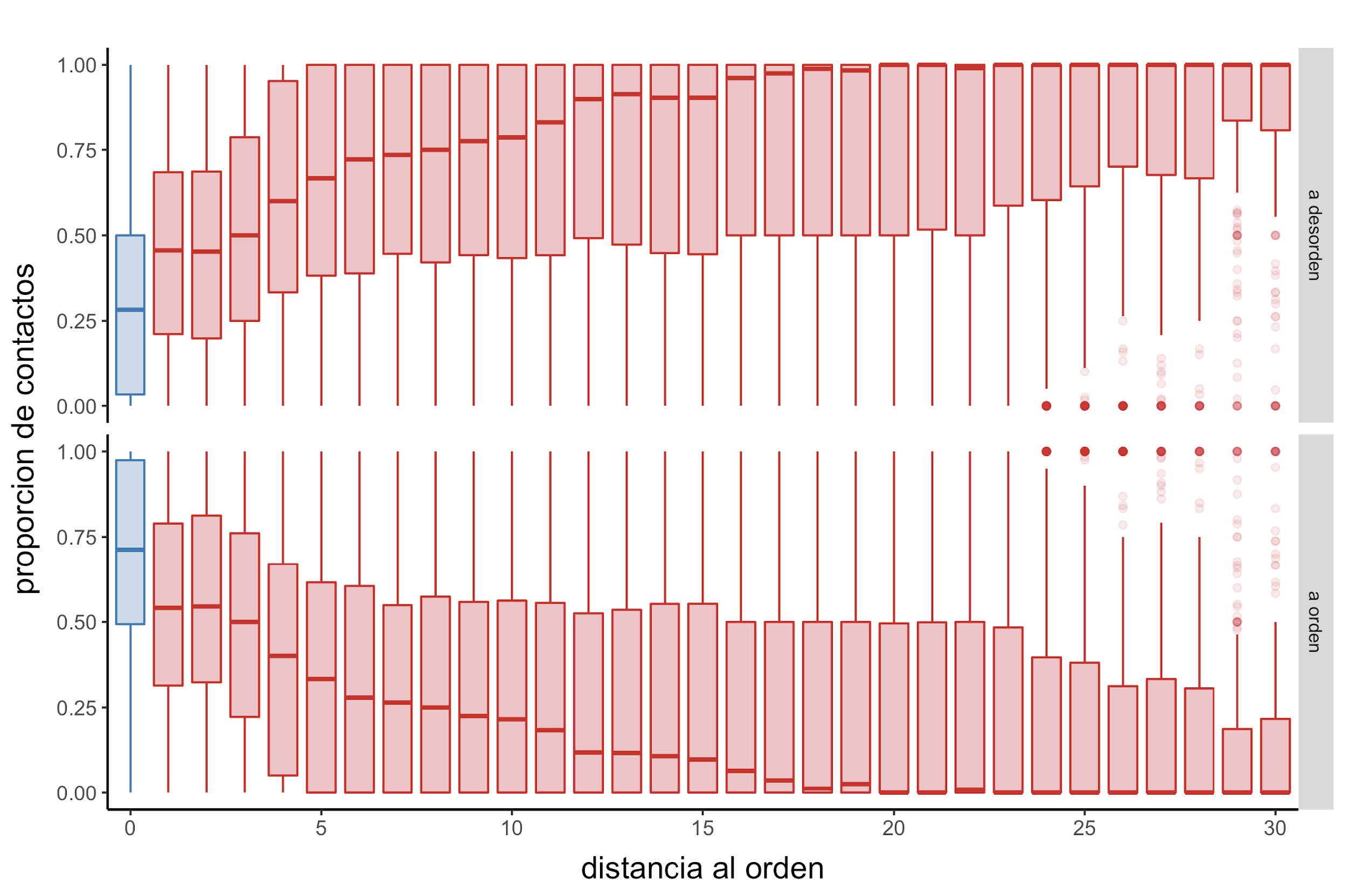
Figura 14: Distribución de la proporción de contactos
Diagramas de caja que muestran la distribución de la proporción de contactos establecidas con posiciones desordenadas (parte superior) o posiciones ordenadas (parte inferior) en función a la distancia secuencial con el residuo ordenado más cercano.
Se observa entonces que el entorno estructural donde se encuentra una posición desordenada (establecida por su distancia secuencial a regiones ordenadas) tienen un gran impacto sobre las velocidades de evolución normalizada, sobre el RMSF y sobre el promedio de contactos para esa posición, influyendo incluso en la proporción de contactos hacia posiciones ordenadas. Con todo lo planteado se puede concluir que las restricciones que imponen las regiones ordenadas en las velocidades de evolución para mantener una estructura tridimensional dada también son impuestas por el desorden en pos de mantener una estructura dinámica, que es clave en el rol biológico de las IDPs.
Todos los resultados descriptos en esta sección que involucran información derivada de contactos como métricas estructurales (promedio, robustez, moda, máximo y mínimo) fueron calculados excluyendo a aquellos contactos que estuvieran establecidos entre residuos que se encontraran distanciados a menos de 4 residuos secuencialmente consecutivos. De esta manera se elimina la posibilidad de que las restricciones impuestas no estuvieran provocadas por el desorden, sino por la aparición de elementos de estructura secundaria transitoria debida al establecimiento de interacciones locales. Las tendencias observadas son las mismas a las informadas en esta sección, los resultados no se abordan en este trabajo.
Evaluación de la información estructural en ensembles mediante velocidades de evolución
Para poder explorar con mayor detalle cómo es la relación entre los ensembles conformacionales de IDPs y las velocidades de evolución, se busca determinar si las velocidades de evolución sitio-específicas correlacionaban mejor con los contactos para cualquier confórmero individual o con la información de contactos promediada a lo largo de todo el ensemble. Para ello, para cada proteína se calcula la correlación de Pearson (derivando el coeficiente de correlación rho (ρ)) entre la velocidad de evolución sitio-específica para una posición y una métrica estructural, en particular el promedio de contactos y la robustez. Luego, se compara con cuál de estos dos descriptores las velocidades de evolución obtienen una mejor correlación.
Para el 75% de las proteínas del conjunto de datos utilizado, la correlación más fuerte se logra cuando se tiene en cuenta la información estructural de una sola conformación (en promedioρ= -0.3692). Podría esperarse que las restricciones funcionales relevantes a la evolución estuviesen impuestas por aquellas conformaciones que tienen el mayor número de contactos (que se asume que es la conformación más cercana a una conformación cerrada de la proteína) o por aquellas conformaciones que poseen el mínimo número de contactos (posiblemente la forma abierta de la proteína). Sin embargo, nuestros resultados indican que las conformaciones cerradas y abiertas no muestran los mejores coeficientes de correlación. En el 25% restante de las proteínas, la mejor correlación se obtiene con parámetros que dan cuenta de la distribución de contactos a lo largo del ensemble completo: en el 21% (promedio ρ = -0.5448) de las proteínas, la mejor correlación se logra con la robustez de contactos mientras que para el ~3%, la mejor correlación se obtiene con el promedio de contactos (promedio ρ = -0.4683). Estos resultados indican que para un cuarto de las proteínas del conjunto de datos, la consideración de la información estructural presente en todo el ensemble permite una mejor explicación sobre los cambios evolutivos observados en el conjunto de proteínas homólogas.
Ahora bien, las correlaciones hasta este punto fueron hechas considerando una sola conformación o bien todo el ensemble, la siguiente pregunta entonces es: ¿existen combinaciones entre 1 y N (donde N es el número de conformaciones totales presentes en el ensemble) que tengan información estructural derivada de contactos que expliquen mejor los perfiles de velocidad observados? En un trabajo realizado anteriormente (Marchetti, Monzon, Tosatto, Parisi, Fornasari, 2019), se demostró que los ensembles de IDPs son redundantes en término de la restricción estructural impuesta en la evolución, debido a que solamente se necesitan alrededor de 10 confórmeros en promedio para explicar la restricción estructural presente en alineamiento de proteínas homólogas de IDPs. Tomando esta idea como directriz, se exploran todas las combinaciones posibles entre los distintos confórmeros para cada ensemble del conjunto de datos, para estudiar si existe un sub-conjunto de conformaciones en particular que de lugar a mejores valores de correlación entre alguna métrica y las velocidades de evolución normalizadas. Para esto, se obtienen todas las combinaciones posibles entre cualquier confórmero en cada ensemble del conjunto de datos. Lo que se combina es la información estructural para cada residuo (ya sea el promedio de contactos o la robustez) de los confórmeros que fueron seleccionados. Luego, se calcula el coeficiente de correlación de Pearson (rho ρ) entre las velocidades de evolución y el promedio de los contactos (referido de aquí en adelante como ρave) y el coeficiente para la correlación entre las velocidades de evolución y la robustez (referido de aquí en adelante como ρcrob). Se obtiene la significancia estadística para cada combinación utilizando una prueba t de student (t-test) que determina si la distribución de los coeficientes ρ es diferente a la distribución de coeficientes generados por distribuciones al azar, que se realizaron mediante un bootstrapping (para más detalles, véase la sección “Métodos”).
Se observa que en ~52% de las proteínas, las velocidades de evolución tienen mejor correlación con la fracción de contactos de los confórmeros combinados (promedio de los coeficientes ρcrob = -0.5254) que con cualquier otra información disponible para confórmeros individuales o parámetros de información estructural derivados de todo el ensemble. En el mismo sentido, para el ~30% de los casos, las correlaciones entre el número promedio de los contactos para una determinada combinación (promedio de los coeficientes ρave = -0.4154), da mejores valores de correlación que el resto de los parámetros, ya sea para un confórmero individual o información promediada a lo largo de todo el ensemble. Solo para el ~17%, de los ensambles conformacionales estudiados la mejor correlación entre las velocidades de evolución y la información de contactos está dada para un confórmero individual, arrojando los valores más bajos de correlación obtenidos promedio ρindiv = -0.3695. En la Tabla 1 puede verse un esquema que resume los valores de correlación obtenidos.

Tabla 1: Valores de los promedios de correlación obtenidos para confórmeros individuales y para un subconjunto de confórmeros Entre paréntesis se muestran los porcentajes de proteínas del conjunto de datos para las cuales esa condición daba la mejor correlación.
Tanto para la fracción o robustez de contactos como para el promedio, la correlación puede ser maximizada si se tiene en cuenta la información contenida en un subconjunto de conformaciones presentes en el ensemble. Estadísticamente se esperaría que a medida que el espacio combinatorio aumente sea más probable que la mejor correlación aparezca por azar (por ejemplo, la mejor correlación debería encontrarse cuando se combinan 10 confórmeros en ensembles con 20 conformaciones distintas). Sin embargo, la mejor correlación entre la fracción o robustez de contactos y las velocidades de evolución se obtuvo cuando se combinaban en promedio 4 confórmeros, mientras que la mejor correlación entre el promedio del número de contactos y las velocidades de evolución se obtuvo cuando se combinaban en promedio 2.8 confórmeros. Nunca se obtuvieron mejores valores de correlación cuando se combinaban más de 8 conformaciones (Figura 15).
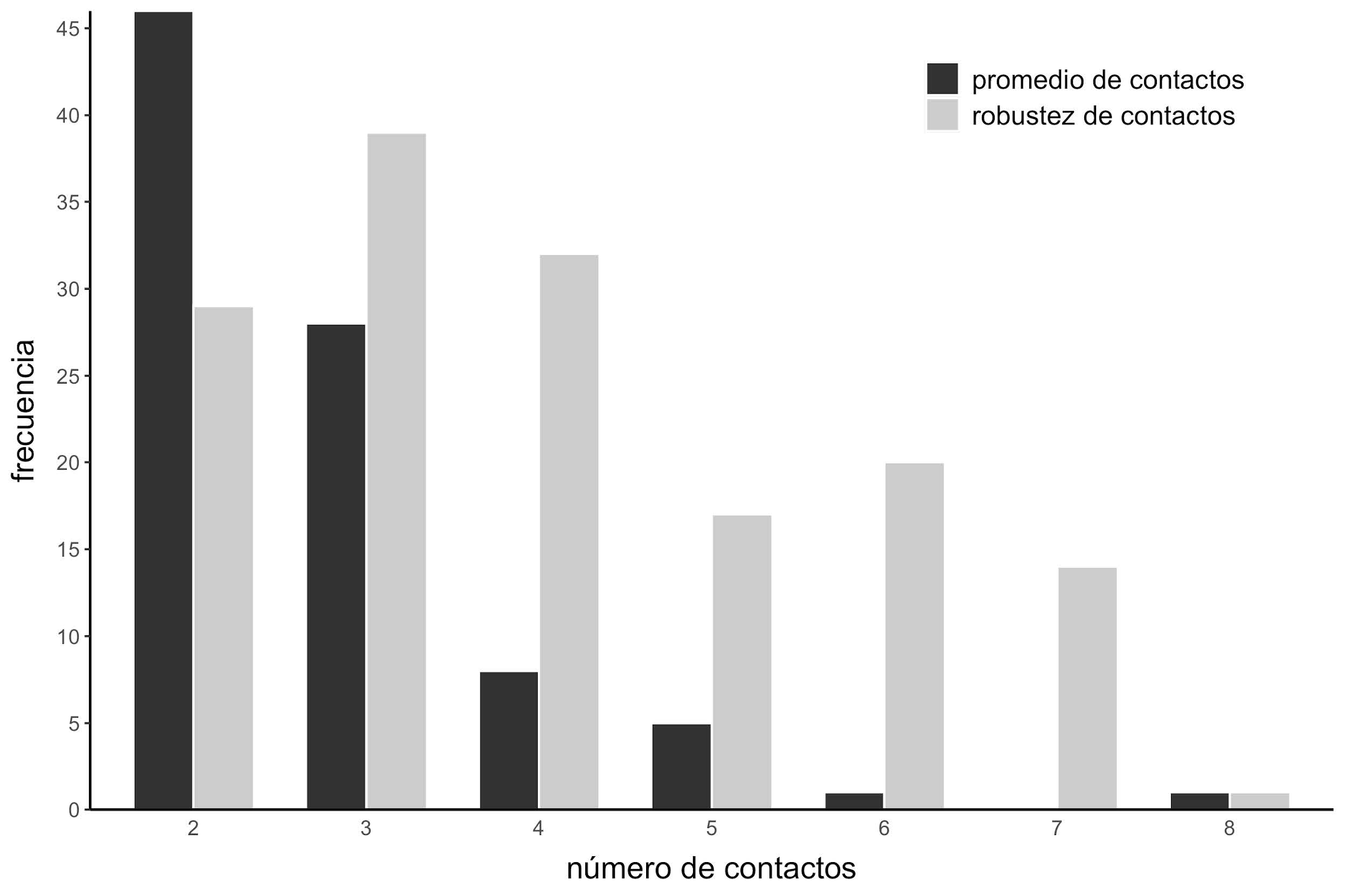
Figura 15: Conformaciones necesarias para la obtención de la mejor correlación. Histograma que muestra el número de diferentes confórmeros necesarios para obtener la mejor combinación entre las velocidades de evolución normalizadas y la robustez (en color gris) y el promedio de número de contactos (en negro).
Todos estos resultados sugieren que la información estructural proveniente de la combinación de determinados confórmeros es idónea para explorar tanto la diversidad conformacional de proteínas, así como su importancia biológica, en concordancia con lo expresado en trabajos previos (Marchetti, Monzon, Tosatto, Parisi, Fornasari, 2019). Estos resultados remarcan la importancia y el peso que tiene el ensemble conformacional sobre las velocidades de evolución ya que la correlación mejoró notablemente cuando se tuvieron en cuenta diferentes descriptores de los contactos en el ensemble conformacional y cuando se obtuvieron combinaciones de confórmeros. Dichas mejoras alcanzaron un 83% de las proteínas estudiadas.
La siguiente pregunta a responder es: ¿por qué para algunas proteínas la mejor correlación se obtiene con la robustez de contactos, mientras que para otras se logra con el promedio de los contactos? Es importante tener en cuenta que la robustez de contactos puede ser una buena métrica estructural para representar a IDPs que tienen una variación estructural considerable entre los confórmeros, de ahí que el número de contactos varíe notablemente entre confórmeros. Por otro lado, el promedio de los contactos puede capturar el comportamiento del ensemble cuando los contactos muestran una variación menor entre confórmeros. En la Figura 16 se ilustran representantes de ambos tipos de proteínas.
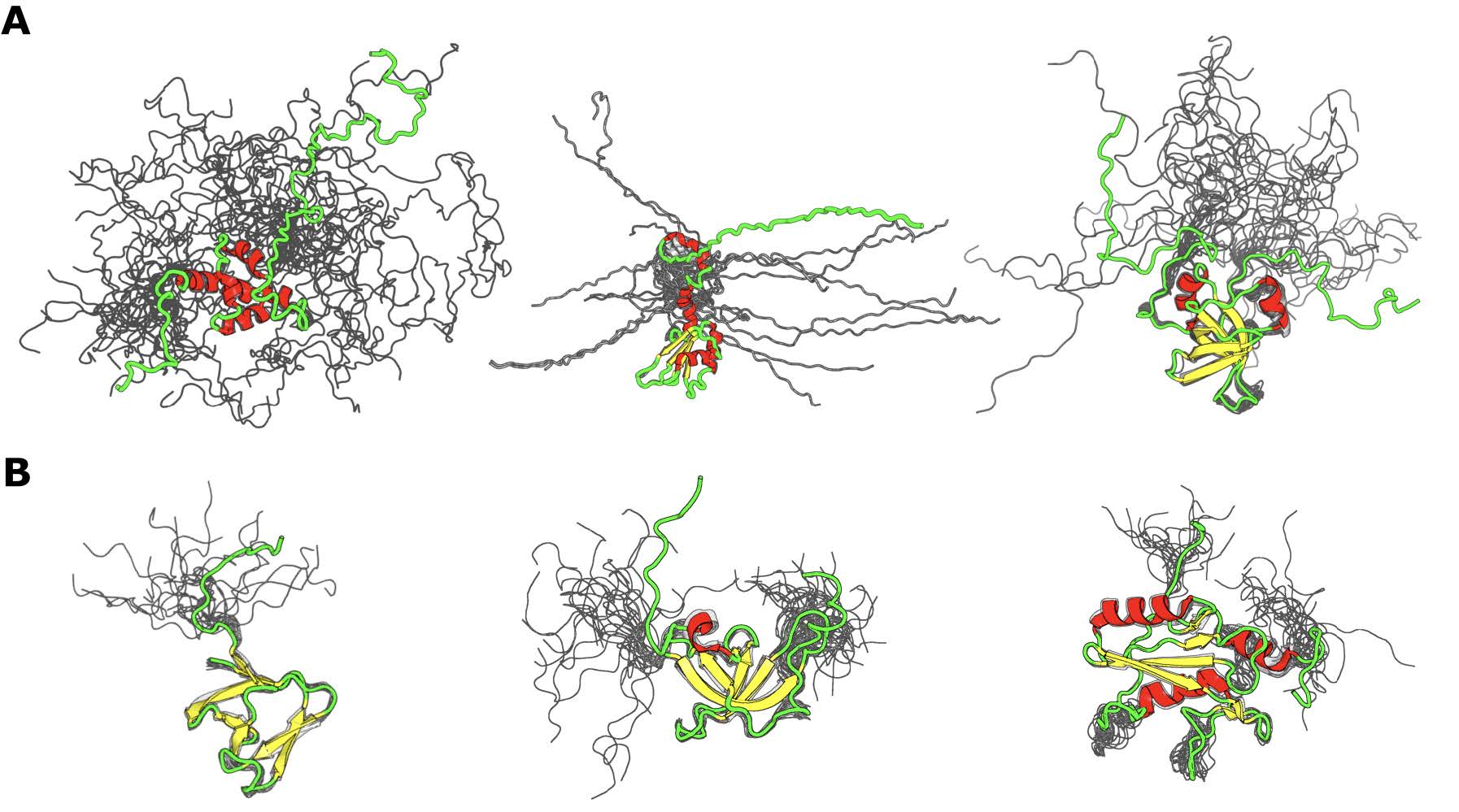
Figura 16: Representación de ensembles proteicos para cada grupo de correlación Representación de ensembles proteicos para las cuales la mejor correlación fue obtenida si se combinaba la información estructural de 2 o más confórmeros. Panel A: ejemplos de ensembles de IDPs para las cuales la fracción de contactos arroja el mejor valor de correlación. De izquierda a derecha códigos PDB: 1G9L_A (dominio PABC de la proteína de unión poly(a) humana), 2M70_A (Citrus sinensis proteína de unión a poli (A) 1), 1D7Q_A (factor de iniciación de traducción humano EIF1A). Panel B: Ejemplos de ensembles de IDPs para los cuales el promedio de los contactos correlaciona mejor con la velocidad normalizada de evolución (de izquierda a derecha códigos PDB: 2KRS_A (Dominio SH3 de Clostridium perfringens putativo de la enterotoxina CPF_0587), 2BUD_A (Dominio cromo putativo de Drosophila melanogaster de machos, ausente en la primera proteína (MOF), 2EO6_A dominio SH2 de ratón de la proteína enlazadora de células B BLNK).
Se planteó como hipótesis que las proteínas que presentan la mejor correlación con la fracción de contactos (como las que se muestran en la Figura 16, panel A) pueden llegar a ser más flexibles y sus posiciones, que están evolutivamente restringidas, pueden establecer contactos en determinado confórmeros y no en otros. En cambio, las proteínas que presentan una mejor correlación con el promedio de los contactos (como se muestra en la Figura 16, panel B), son estructuras que son más cerradas, donde el número de contactos en cada posición se mantiene en las distintas conformaciones del ensemble. Con el fin de probar esta hipótesis se estimó el valor de RMSD y el radio de giro entre todos los confórmeros en el ensemble y se calcularon sus valores máximo, mínimo y promedio. El radio de giro es una medida que aporta información sobre el grado de compactación de una proteína.
Se observa que para el conjunto de proteínas en donde la robustez de contactos provee la mejor correlación con las velocidades de evolución, el promedio del promedio de RMSD es de 19.77 Å y el promedio de los RMSD máximos es 35.2 Å, mientras que el promedio del valor de radio de giro medio en el ensemble es 23.13Å. Para el conjunto de proteínas que muestran la mejor correlación con el promedio de los contactos y la velocidad de evolución, se observan valores más bajos de RMSD: el promedio del promedio es 11.12 Å y el promedio de los máximos es 20.28 Å. También resultan valores más bajos de radio de giro, con promedio de 18.27Å (Tabla 2). Tanto el RMSD como el radio de giro en el ensemble dan evidencia extra para respaldar la hipótesis planteada según la cual cuando las velocidades de evolución son mejor explicadas con el promedio de los contactos, deben presentar conformaciones menos extendidas y menos flexibles.
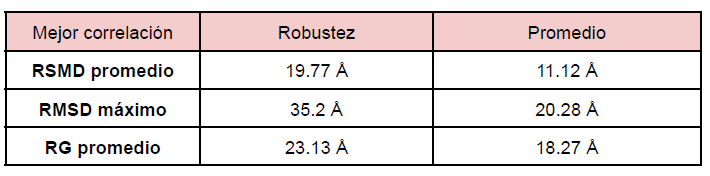
Tabla 2: Valores de RMSD promedio, RMSD máximo y RG promedio para las mejores correlaciones obtenidas con la robustez de contactos o el promedio
En una primera aproximación, la heterogeneidad de las velocidades de evolución en las IDPs (véanse Figura 2, Figura 3, Figura 11) puede ser explicada como función de los contactos terciarios por posición en los distintos confórmeros del ensemble (véanse Figura 5, Figura 9, Figura 10, Figura 13). Estos resultados sugieren que el estado del arte y todo lo que se conoce hasta el momento en relación con las tasas evolutivas de proteínas globulares puede extenderse a proteínas que carecen de una estructura estable y definida como las IDPs. Sin embargo, este tipo de proteínas, como ya se describió, poseen ciertas particularidades. La mayor diferencia entre las proteínas globulares y las IDPs es la enorme diversidad estructural que las últimas presentan entre los distintos confórmeros que forman parte del ensemble nativo. Este comportamiento particular implica una variabilidad muy marcada en el número de contactos por sitio en cada confórmero.
Las variaciones en la cantidad de contactos por posición debido a cambios conformacionales fueron extensamente ignoradas en los estudios evolutivos (excepto en algunos ejemplos como Zea, Monzon, Fornasari, Marino-Buslje, Parisi (2013) y Sharir-Ivry, Xia (2017)). Pero, como se deduce de este artículo, son imposibles de negar en los ensembles de IDPs. Estas variaciones imponen restricciones acumulativas en las velocidades de evolución (Saldaño, Monzon, Parisi, Fernandez-Alberti, 2016) que podrían reflejar la importancia de las conformaciones transitorias o preferentes en el ensemble (Davey, 2019). Es posible que la heterogeneidad de la velocidad de evolución en regiones desordenadas se deba parcialmente a la presencia de módulos funcionales involucrados en interacciones proteína-proteína, unión a ligando o modificaciones post-traduccionales. Entre estos, los motivos lineales cortos (Short Linear Motivs, o SLiMs por sus siglas en inglés) son sitios típicos de interacción en IDPs, y usualmente se encuentran más conservados que los residuos a su alrededor (van der Lee et al., 2014). Si bien no se detectaron sitios de unión cuando se buscaron SLiMs conocidos en la base de datos ELM (Gouw et al., 2018), podrían existir conformaciones ‘predilectas’ que llegarían a contener estructuras secundarias residuales relacionadas con las interacciones entre proteínas.
Las IDPs presentes en este conjunto de datos tienen diferentes patrones estructurales con alternancia entre regiones ordenadas y desordenadas que son evidenciadas en los perfiles de velocidad. Dado que estos perfiles reflejan la preferencia por determinadas conformaciones, podrían ser usados para inferir y clasificar comportamientos globales de IDPs. A su vez, se observa que existe una relación entre las velocidades de evolución y la cercanía con regiones ordenadas, dando cuenta de los efectos moduladores que tienen los dominios plegados o estructurados en las velocidades de evolución de regiones desordenadas adyacentes, dando lugar a la pregunta sobre la ocurrencia de procesos de coevolución (Mittal, Holehouse, Cohan, Pappu, 2018) en IDPs.
Estos resultados sugieren que los estudios estructurales con base evolutiva sobre IDPs no solo son posibles sino que también son una aproximación que promete revelar importante información sobre la evolución y la biología de proteínas intrínsecamente desordenadas.
El conjunto de datos utilizados se construyó a partir de IDPs que estuvieran depositadas en la PDB (Rose et al., 2015) y que, por lo tanto, su estructura fuese conocida y obtenida mediante técnicas de NMR. Para tal fin, se descargaron todos los archivos de coordenadas estructurales obtenidos por NMR y sobre ese conjunto se predijo el porcentaje de desorden con el método ESpritz (Walsh, Martin, Di Domenico, Tosatto, 2012) y se clasificaron como IDPs aquellas proteínas que tuviesen al menos un 40% de sus residuos predichos como desordenados. A continuación se obtuvieron alineamientos múltiples de proteínas homólogas presentes en la base de datos HSSP (Dodge, Schneider, Sander, 1998), filtrando y seleccionando aquellos MSA que tuviesen solo un ~5% de gaps en promedio por posición y con porcentajes de identidad entre el 33 y el 100% contra la secuencia de referencia de PDB, y que tuviesen una cobertura de al menos el 60% con esta última (median identity percentage de 64%). Los alineamientos utilizados tenían en promedio 96 secuencias y un promedio de de 7.38% de gaps en las posiciones. Para asegurarse que en el conjunto de datos consistía en proteínas que fueran menos del 50% idénticas, se utilizó el programa CD-HIT (Fu, Niu, Zhu, Wu, Li, 2012).Todas las proteínas que cumpliesen con estas condiciones fueron posteriormente inspeccionadas visualmente y se seleccionaron aquellas que tuviesen un contenido de desorden evidente en la estructura 3D. Este paso es importante porque los predictores pueden, como todo método, tener errores en la asignación de desorden. Además, en esta instancia se eliminaron proteínas quiméricas.
El conjunto de datos final y curado consistió en 310 IDPs, con una longitud promedio de aproximadamente 130 residuos (mínimo 58, máximo 37), y número promedio de confórmeros por ensemble de aproximadamente 20 (mínimo 6, máximo 60). En este conjunto de datos las regiones desordenadas que consisten de más de 5 residuos tienen una longitud promedio de 23.6 aminoácidos, con un máximo de 263. Pueden observarse algunas de las IDPs utilizadas para el estudio en la Figura 17.
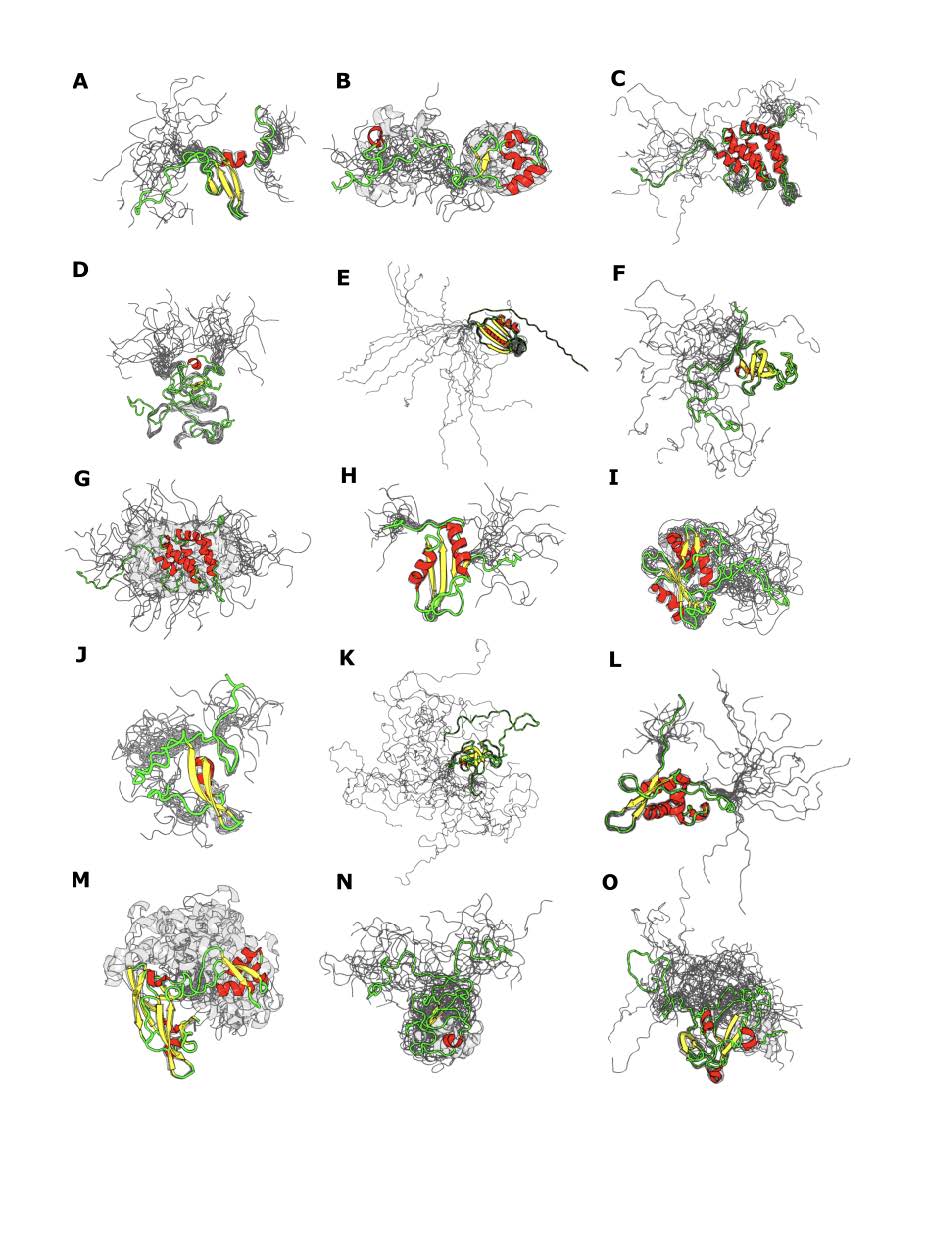
Figura 17: Representación de IDPs presentes en el conjunto de datos. Códigos PDB: a) 1AP0_A, b) 1WWK_A, c) 1INZ_A, d) 1IXD_A, e) 2LXF_A, f) 2COY_A, g) 1EJ5_A, h) 2DGQ_A, i) 2BBU_A, j) 2JZ6_A, k) 2CP5_A, l) 2KPM_A, m) 2L9Y_A, n) 1JFN_A, o) 2N1I_A.
Estimación de las velocidades de evoluciónPara el cálculo de las velocidades de evolución se utilizó el programa Rate4Site (Pupko, Bell, Mayrose, Glaser, Ben-Tal, 2002) con los alineamientos descritos previamente. Este programa estima las velocidades de evolución sitio-específicas mediante métodos Bayesianos bajo la hipótesis de independencia entre los sitios, reconstruye un árbol filogénetico para las secuencias del MSA mediante un algoritmo de unión de vecinos (neighbor-joining y NJ por su sigla en inglés) y distancias estimadas por máxima verosimilitud. En este trabajo se utilizó el modelo de JTT (Jones, Taylor, Thornton, 1992). Para cada proteína, los valores de velocidad de evolución sitio-específicos crudos del Rate4Site se normalizaron dividiéndolos por el valor promedio de velocidad de la proteína entera tal como se indica en Sydykova, Wilke (2017). El test de Wilcoxon fue utilizado para evaluar las diferencias significativas en las medias de las velocidades de evolución normalizadas entre los subconjuntos de posiciones ordenadas y desordenadas.
Todos los resultados comentados en esta sección que involucran información derivada de contactos como métricas estructurales (promedio, robustez, moda, máximo y mínimo) fueron derivados para cada confórmero de cada ensemble nativo de IDPs presente en el conjunto de datos, y la información de contactos fue obtenida como el valor absoluto de los contactos terciarios por posición, definido como la distancia mínima entre las esferas de Van der Waals, para cualesquiera dos átomos pesados de las cadenas laterales de los aminoácidos, utilizando un valor de corte de 1.0 Å (Berrera, Molinari, Fogolari, 2003). Estas métricas fueron estimadas de distintas maneras: el promedio, la moda, el máximo y el mínimo número de contactos por posición fueron calculados sobre una misma posición a lo largo de todo el ensamble. La fracción o robustez de contactos por posición fue definida y calculada como la fracción de confórmeros que tienen al menos un contacto para esa posición. Por ejemplo, un valor de robustez 0.5 (o del 50%) significa que la mitad de los confórmeros observados tiene al menos un contacto en esa posición (véase Figura 3.7). Para cada posición desordenada, la distancia a un residuo ordenado fue calculada como la mínima distancia consecutiva al residuo ordenado más cercano. La flexibilidad fue estimada usando el RMSF de los Cα, calculados según MIToS (Zea, Anfossi, Nielsen, Marino-Buslje, 2017). Los valores de RMSF fueron normalizados, dividiendo los valores RMSF de cada posición por el promedio de los RMSF del ensamble. El mismo paquete fue utilizado para calcular los valores de RMSD de toda la proteína.
Obtención de los perfiles de velocidad y patrones conformacionalesPara cada proteína en el conjunto de datos se estimó su velocidad de evolución y los perfiles de RMSF por posición, y se derivaron las respectivas medidas normalizadas. Como las proteínas tienen longitudes distintas, para poder hacer comparaciones válidas entre ellas las posiciones fueron renumeradas al rango [0,1], dividiendo cada posición por la longitud total de la proteína. De esta manera, para cada proteína fue posible obtener patrones individuales como los ilustrados en la Figura 18. Se corroboraron visualmente los arreglos de orden/desorden en los elementos estructurales de cada proteína para poder definir sus patrones estructurales, y los perfiles individuales fueron luego agrupados y acumulados en función de las organizaciones estructurales de desorden antes mencionadas. Esto resulta en los perfiles ilustrados en la Figura 3. Se realizó una regresión LOESS suavizada para poder modelar el comportamiento y la variabilidad de la información (véase la línea azul de la Figura 3).
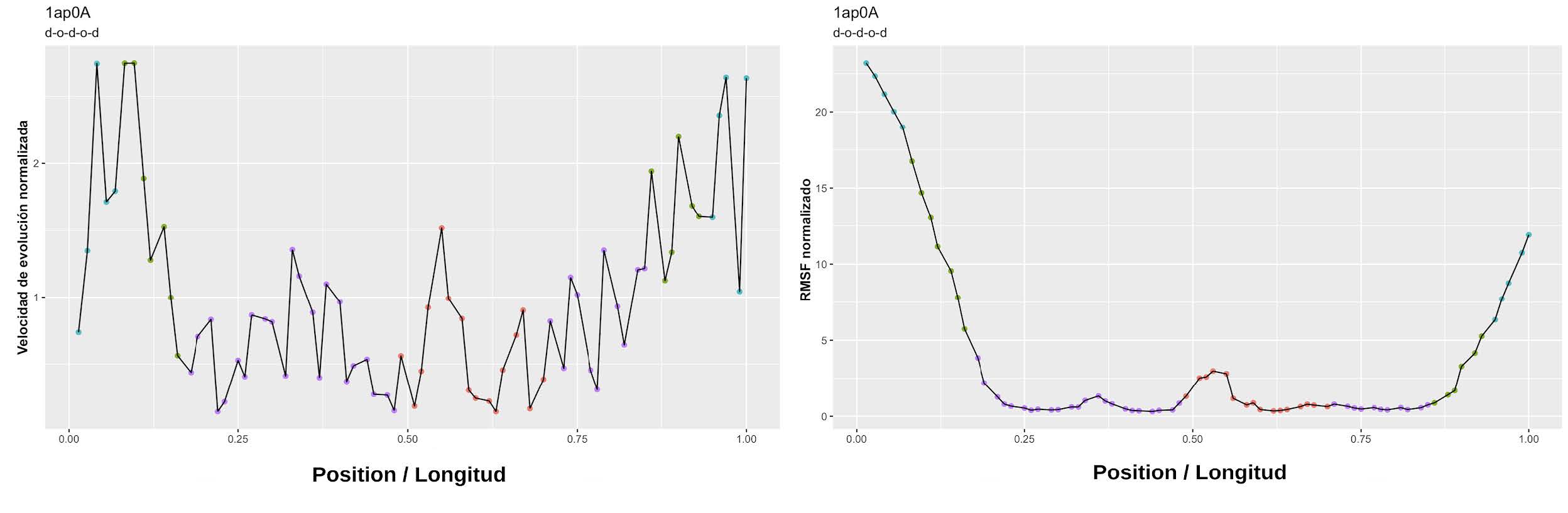
Figura 18: Perfiles individuales de velocidad de evolución normalizada y RMSF normalizado. Se muestra un perfil individual para la velocidad normalizada (izquierda) y un perfil de RMSF normalizado (derecha). En el eje x se grafica la posición normalizada de la longitud para poder acumular los perfiles de proteínas distintas. Este perfil corresponde al dominio de enlace de cromatina (Cromo) de la proteína modificadora 1 de ratón (código PDB: 1AP0_A). Esta proteína tiene 2 regiones ordenadas flanqueadas por regiones desordenadas, tal como queda evidenciado en el perfil de velocidad (izquierda) y el de RMSF (derecha).
Berlow R. B., Dyson H. J., Wright P. E. (2015). Functional advantages of dynamic protein disorder. FEBS Lett. 589(19 Pt A), pp. 2433–40.
Berrera M., Molinari H., Fogolari F. (2003). Amino acid empirical contact energy definitions for fold recognition in the space of contact maps. BMC Bioinformatics 4, p. 8.
Brown C. J., Takayama S., Campen A. M., Vise P., Marshall T. W., Oldfield C. J., (et al.). Evolutionary rate heterogeneity in proteins with long disordered regions. Journal Molecular Evolucion 55(1), pp. 104–10. DOI: 10.1007/s00239-001-2309-6
Davey N. E. (2019). The functional importance of structure in unstructured protein regions. Curr Opin Struct Biol 56, pp. 155–63. DOI: 10.1016/j.sbi.2019.03.009
Dodge C., Schneider R., Sander C. (1998). The HSSP database of protein structure-sequence alignments and family profiles. Nucleic Acids Res. 26(1), pp. 313–5. DOI: 10.1093/nar/26.1.313
Dosztányi Z., Csizmók V., Tompa P., Simon I. (2005). The pairwise energy content estimated from amino acid composition discriminates between folded and intrinsically unstructured proteins. J Mol Biol. 347(4), pp. 827–39. DOI: 10.1016/j.jmb.2005.01.071
Drummond D. A., Bloom J. D., Adami C., Wilke C. O., Arnold F. H. (2005). Why highly expressed proteins evolve slowly. Proc Natl Acad Sci USA. 102(40), pp. 14338–43. DOI: 10.1073/pnas.0504070102
Echave J., Spielman S. J., Wilke C. O. (2016). Causes of evolutionary rate variation among protein sites. Nat Rev Genet 17(2), pp. 109–21. DOI: 10.1038/nrg.2015.18
Franzosa E. A., Xia Y. (2009). Structural determinants of protein evolution are context-sensitive at the residue level. Mol Biol Evol. 26(10), pp. 2387–95. DOI:10.1093/molbev/msp146
Fu L., Niu B., Zhu Z., Wu S., Li W. (2012). CD-HIT: accelerated for clustering the next-generation sequencing data. Bioinformatics 28(23), pp. 3150–2. DOI: https://doi.org/10.1093/bioinformatics/bts565
Gerstein M., Krebs W. (1998). A database of macromolecular motions. Nucleic Acids Res 26(18), pp. 4280–90. DOI: 10.1093/nar/26.18.4280
Gouw M., Michael S., Sámano-Sánchez H., Kumar M., Zeke A., Lang B., et al. (2018). The eukaryotic linear motif resource - 2018 update. Nucleic Acids Res, 46(D1), pp. D428–34. DOI: 10.1093/nar/gkx1077
Hammes G. G., Chang Y-C., Oas T. G. (2009). Conformational selection or induced fit: a flux description of reaction mechanism. Proc Natl Acad Sci USA 106(33), pp. 13737–41. DOI: https://doi.org/10.1073/pnas.090719510
Jones D.T., Taylor W. R., Thornton J. M. (1992). The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci 8(3), pp. 275–82. DOI: 10.1093/bioinformatics/8.3.275
Lobanov M. Y., Galzitskaya O. V. (2015). How common is disorder? occurrence of disordered residues in four domains of life. Int J Mol Sci, 16(8), pp. 19490–507. DOI: 10.3390/ijms160819490
Marchetti J., Monzon A. M., Tosatto S. C. E., Parisi G., Fornasari M. S. (2019). Ensembles from Ordered and Disordered Proteins Reveal Similar Structural Constraints during Evolution. J Mol Biol 431(6), pp. 1298–307. DOI: 10.1016/j.jmb.2019.01.031
Mészáros B., Dobson L., Fichó E., Tusnády G. E., Dosztányi Z., Simon I. (2019). Sequential, structural and functional properties of protein complexes are defined by how folding and binding intertwine. J Mol Biol 431(22), pp. 4408–28. DOI: 10.1016/j.jmb.2019.07.034
Mittal A., Holehouse A. S., Cohan M. C., Pappu R. V. (2018). Sequence-to-Conformation Relationships of Disordered Regions Tethered to Folded Domains of Proteins. J Mol Biol 430(16), pp. 2403–21. DOI: https://doi.org/10.1016/j.jmb.2018.05.012
Monzon A. M., Rohr C. O., Fornasari M. S., Parisi G. (2016). CoDNaS 2.0: a comprehensive database of protein conformational diversity in the native state. Database (Oxford) . DOI: 10.1093/database/baw038
Monzon A. M., Zea D. J., Fornasari M. S., Saldaño T. E., Fernandez-Alberti S., Tosatto S.C.E. (et al.). (2017). Conformational diversity analysis reveals three functional mechanisms in proteins. PLoS Comput Biol, 13(2), e1005398. DOI: https://doi.org/10.1371/journal.pcbi.1005398
Necci M., Piovesan D., Tosatto S.C.E. (2016). Large-scale analysis of intrinsic disorder flavors and associated functions in the protein sequence universe. Protein Sci. 25(12), pp. 2164–74. DOI: 10.1002/pro.3041
Nussinov R., Ma B., Tsai C-J. (2014). Multiple conformational selection and induced fit events take place in allosteric propagation. Biophys Chem 186, pp. 22–30. DOI: 10.1016/j.bpc.2013.10.002
Pancsa R., Zsolyomi F., Tompa P. (2018). Co-Evolution of Intrinsically Disordered Proteins with Folded Partners Witnessed by Evolutionary Couplings. Int J Mol Sci 19(11). DOI: https://doi.org/10.3390/ijms19113315
Prakash A., Shin J., Rajan S., Yoon H. S. (2016). Structural basis of nucleic acid recognition by FK506-binding protein 25 (FKBP25), a nuclear immunophilin. Nucleic Acids Res 44(6), PP. 2909–25. DOI: 10.1093/nar/gkw001
Pupko T., Bell R. E., Mayrose I., Glaser F., Ben-Tal N. (2002). Rate4Site: an algorithmic tool for the identification of functional regions in proteins by surface mapping of evolutionary determinants within their homologues. Bioinformatics 18 Suppl 1, S71-7. DOI: 10.1093/bioinformatics/18.suppl_1.s71
Reisen F., Weisel M., Kriegl J.M., Schneider G. (2010). Self-organizing fuzzy graphs for structure-based comparison of protein pockets. J Proteome Res 9(12), pp. 6498–510. DOI: 10.1021/pr100719n
Robinson M. A., Park S., Sun Z-YJ., Silver P.A., Wagner G., Hogle J. M. (2005). Multiple conformations in the ligand-binding site of the yeast nuclear pore-targeting domain of Nup116p. J Biol Chem 280(42), pp. 35723–32. DOI: 10.1074/jbc.M505068200
Rose P.W., Prlić A., Bi C., Bluhm W. F., Christie C.H., Dutta S., et al. (2015). The RCSB Protein Data Bank: views of structural biology for basic and applied research and education. Nucleic Acids Res 43(Database issue), D345-56. DOI: 10.1093/nar/gku1214
Saldaño T. E., Monzon A. M., Parisi G., Fernandez-Alberti S. (2016). Evolutionary conserved positions define protein conformational diversity. PLoS Comput Biol12(3), e1004775.DOI: 10.1371/journal.pcbi.1004775
Samsudin F., Gan SK-E, Bond PJ. (2020). The Structural Basis for Gag Non-Cleavage Site Mutations in Determining HIV-1 Viral Fitness. BioRxiv. DOI: https://doi.org/10.1101/2020.07.05.188326
Sharir-Ivry A., Xia Y. (2017). The impact of native state switching on protein sequence evolution. Mol Biol Evol. 34(6), pp. 1378–90. DOI: 10.1093/molbev/msx071
Shimojo H., Kawaguchi A., Oda T., Hashiguchi N., Omori S., Moritsugu K., et al. (2016). Extended string-like binding of the phosphorylated HP1α N-terminal tail to the lysine 9-methylated histone H3 tail. Sci Rep. 6, 22527. DOI: https://www.nature.com/articles/srep22527
Sydykova D.K., Wilke C.O. (2017). Calculating site-specific evolutionary rates at the amino-acid or codon level yields similar rate estimates. PeerJ., 5, e3391. DOI: https://doi.org/10.7717/peerj.3391
The UniProt Consortium (2017). UniProt: the universal protein knowledgebase. Nucleic Acids Res, 45(D1), D158–69.
Toth-Petroczy A., Palmedo P., Ingraham J., Hopf T.A., Berger B., Sander C., et al. (2016). Structured States of Disordered Proteins from Genomic Sequences. Cell. , 167(1), 158-170.e12. DOI: https://doi.org/10.1016/j.cell.2016.09.010
Tóth-Petróczy A., Tawfik DS. (2011). Slow protein evolutionary rates are dictated by surface-core association. Proc Natl Acad Sci USA 108(27), pp. 11151–6. DOI: https://doi.org/10.1073/pnas.1015994108
Uversky V.N., Oldfield C.J., Midic U., Xie H., Xue B., Vucetic S., et al. (2009). Unfoldomics of human diseases: linking protein intrinsic disorder with diseases. BMC Genomics 10 Suppl 1, S7. DOI: 10.1186/1471-2164-10-S1-S7
van der Lee R., Buljan M., Lang B., Weatheritt R.J., Daughdrill G.W., Dunker A.K., et al. (2014). Classification of intrinsically disordered regions and proteins. Chem Rev 114(13), pp. 6589–631. DOI: https://doi.org/10.1021/cr400525m
Volpon L., D’Orso I., Young C.R., Frasch A.C., Gehring K. (2005). NMR structural study of TcUBP1, a single RRM domain protein from Trypanosoma cruzi: contribution of a beta hairpin to RNA binding. Biochemistry 44(10), pp. 3708–17. DOI: 10.1021/bi047450e
Walsh I., Martin A.J.M., Di Domenico T., Tosatto S.C.E. (2012). ESpritz: accurate and fast prediction of protein disorder. Bioinformatics 28(4), pp. 503–9.
Wei G., Xi W., Nussinov R., Ma B. (2016). Protein ensembles: how does nature harness thermodynamic fluctuations for life? the diverse functional roles of conformational ensembles in the cell. Chem Rev 116(11), pp. 6516–51.
Yeh S-W, Huang T-T, Liu J-W, Yu S-H, Shih C-H, Hwang J-K, et al. (2014). Local packing density is the main structural determinant of the rate of protein sequence evolution at site level. Biomed Res Int. 2014, 572409. DOI: 10.1155/2014/572409
Zea D.J., Anfossi D., Nielsen M., Marino-Buslje C. (2017). MIToS.jl: mutual information tools for protein sequence analysis in the Julia language. Bioinformatics 33(4), pp. 564–5. DOI: https://doi.org/10.1093/bioinformatics/btw646
Zea D.J., Miguel Monzon A., Fornasari M.S., Marino-Buslje C., Parisi G. (2013). Protein conformational diversity correlates with evolutionary rate. Mol Biol Evol 30(7), pp. 1500–3. DOI: http://dx.doi.org/10.1093/molbev/mst065
Zea D.J., Monzon A.M., Gonzalez C., Fornasari M.S., Tosatto S.C.E., Parisi G. (2016). Disorder transitions and conformational diversity cooperatively modulate biological function in proteins. Protein Sci. 25(6), pp. 1138-46. DOI: 10.1002/pro.2931

