Uso de una hoja de signos como “memoria externa” en clases de Álgebra y Geometría Analítica
Using a sign sheet as “external memory” in Algebra and Analytical Geometry classes
Leonardo Javier D’Andrea“La evolución del saber debe concebirse no como un
fenómeno natural sino como un fenómeno cultural”
Radford, 2017, p. 107
Desde una perspectiva histórico cultural en la Educación (Vygotsky, 1934; Hernández Rojas, 1988; Wertsh, 1988; Moll, 1993; Baquero, 1997; Daniels, 2003; Vygotsky, 2012a-2012b-2012c-2012d; Baquero y Limón Luque, 2012) y ubicados en los principios de la Teoría de la Objetivación – TO – (Radford, 2000-2006-2014-2017) sobre la enseñanza y el aprendizaje de la Matemática, se inicia explicitando qué se entiende por saber y por conocimiento: “no podemos entender el aprendizaje si no logramos dar una explicación satisfactoria del objeto de aprendizaje y de la naturaleza de ese objeto” (Radford, 2017, p. 97).
Siguiendo a Radford (2017), el saber es considerado una potencialidad en el sentido aristotélico, por ejemplo el saber algebraico es una potencialidad incrustada en la cultura, brinda “posibilidades a los individuos para pensar, reflexionar, plantear y resolver problemas de cierta manera” (p. 101). Es importante aclarar que no se coloca al saber en una línea platonista, formas universales y atemporales independientes del trabajo humano; sino que “son los propios individuos los que constituyen el saber en potencialidad a través de su propia labor – a través de sus acciones, de sus reflexiones, sus sufrimientos y sus esperanzas” (Radford, 2017, p. 101), tal como se expresa en el epígrafe de este apartado.
De esta manera, se entenderá al saber matemático como “concreción de formas abstractas previas de pensamiento y acción matemáticos, que son lingüísticas, perceptivas, artefactuales y corporales” (Radford, 2017, p. 107). Posteriormente, se define al conocimiento como la actualización o materialización del saber.
El saber es algo general que para existir, debe materializarse a través de un proceso de actualización, el cual denominamos conocimiento, y este último como contenido conceptual concreto aparece o puede aparecer únicamente en una actividad: “la actividad demarca la manera en que el saber se manifiesta en el conocimiento” (Radford, 2017, p. 109).
Desde la TO el conocimiento no es un proceso directo, sino que requiere del aprendizaje, concebido como “el encuentro consciente y deliberado con formas histórica y culturalmente codificadas de pensamiento y acción” (Radford, 2017, p. 133). A diferencia de la noción constructivista, que se centra en el estudiante y el aprendizaje debe emanar de este último, la TO propone una relación docente-estudiante enmarcada por la idea de labor conjunta (véase Figura 1) de naturaleza ética (una orientación genuina no egoísta hacia los otros).
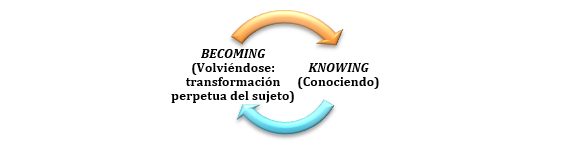
Figura 1: Labor conjunta que ocurre en un espacio socio-político al interior del cual tiene lugar un conociendo –knowing– y el volviéndose –becoming–, esto es volviéndose sujeto en tanto que proyecto histórico-social siempre inconcluso. Fuente: Radford, 2014, p. 135.
“El hombre crea estímulos artificiales y domina
así los propios procesos de su memorización”
Vygotsky, 2012c, p. 79
En línea con lo que plantea el CONFEDI (2014, 2016, 2018) acerca de la enseñanza centrada en el desarrollo de competencias, y en la puesta en práctica de lo mencionado en un trabajo anterior (D’Andrea, 2019a) sobre diseñar de actividades matemáticas en las carreras de Ingeniería desde el Enfoque por Competencias, se propone analizar los alcances y limitaciones de la elaboración y la implementación de una hoja de fórmulas en las clases de Álgebra y Geometría Analítica (AyGA) de la Facultad Regional Avellaneda, Universidad Tecnológica Nacional (FRA-UTN), Argentina.
Basados en la noción vygotskyana de signo, los principios que guían el presente trabajo son que el empleo de signos auxiliares interviene entre el campo sensorial y el sistema motor, posibilitando nuevas formas de conducta; las operaciones con signos requieren un vínculo intermedio entre el estímulo y la respuesta, y dicho estímulo (signo) de segundo orden introducido en la operación cumple la función especial de crear una nueva relación: invierte la acción, ya que opera en el individuo y no en el entorno (Vygotsky, 2012a). El término “introducido” refiere a que el individuo debe estar activamente comprometido a establecer dicho vínculo. De esta manera surge un acto complejo y mediato.
En este sentido, en relación al trabajo de los estudiantes con signos, Gentiletti (2012) - basándose en la psicología cultural - afirma que la toma de apuntes por parte de los estudiantes “colabora en muchos sentidos a la concentración y la percepción discriminada de los elementos centrales del discurso, constituyéndose en la ‘memoria externa’ del desarrollo de una clase” (p. 51).
Durante el año 2019, los docentes de la cátedra AyGA de la FRA-UTN consensuaron proponer a los estudiantes la realización e implementación de una hoja de fórmulas para la instancia evaluativa de las unidades de la materia donde se abordan las nociones de Geometría Analítica: Rectas en el plano, Rectas y Planos en el espacio tridimensional, Cónicas, Superficies (Cuádricas).
Se acordó que el diseño de la hoja tiene la finalidad de incluir todas las fórmulas que se consideren necesarias para la resolución de las actividades que se trabajan en las clases y que puedan colaborar durante la resolución del parcial, a modo de “liberarse” de su memorización (véase el epígrafe de la presente sección).
Desde este acuerdo, un grupo de docentes de la cátedra posicionados en una concepción dialéctica entre enseñanza y aprendizaje como labor conjunta, inmersos en una práctica reflexiva (Perrenoud, 2009; Tobón, 2013) y centrados las competencias de egreso definidas por el CONFEDI (2014, 2016) para las diferentes ingenierías, llevaron a cabo la experiencia de elaborar -en cada curso- el artefacto semiótico en forma colaborativa con el propósito de promover grupalmente el intercambio de visiones personales, poniendo en debate cuáles deben ser los objetos matemáticos por incluir y el modo de formularlos en la hoja.
Entre las competencias genéricas que son la “fuente” desde donde se originan estas actividades, se comprende que las acciones que se desprenderán de estas últimas permiten en forma directa o indirectamente el desarrollo de las primeras. Por ello, se han considerado las competencias sociales, políticas y actitudinales que se exponen en la Tabla 1 (CONFEDI, 2014)
Ver tabla "Competencias genéricas que originan y dirigen la actividad" Fuente: creación propia.
Para tales fines, se comparte en el aula virtual del curso un documento con algunas de las fórmulas a incluir, se vuelve sobre ella en las clases para discutir sobre la comprensión y el posible uso de las anotaciones. Es imprescindible, como afirma Gentiletti (2012), que el diseño se realice en forma paulatina, guiada y grupal, no refleje sólo la voz del docente sino la construcción compartida del conocimiento, porque de esta manera se “favorece la concientización de las producciones discursivas de todos y (…) mejora la capacidad de atención y escucha entre compañeros” (p. 51).
Una de las cuestiones que reguló el trabajo fueron las restricciones que se plantearon desde la cátedra frente a la propuesta, y se explicitaron en las aulas en forma de interrogantes para la discusión entre docentes y estudiantes: ¿cuál es toda la información que podemos incluir en la hoja? ¿Se pueden agregar ejemplos? ¿Pueden o deben escribirse todas y cada una de las fórmulas que se trabajan? ¿Es posible ampliar las fórmulas con definiciones y/o propiedades?
Mercer (1997) afirma que “la información se puede acumular, pero el conocimiento y la comprensión sólo se generan trabajando con la información, seleccionándola, organizándola y discutiendo su importancia” (Gentiletti, 2012, p. 53), y propone estimular en la clase distintos tipos de conversación, como por ejemplo la conversación exploratoria que permite generar interacciones discursivas en las prácticas educativas fomentando la construcción compartida y crítica del conocimiento:
La información que se pone a disposición del grupo no es para hacer ostentación del saber, sino justamente para la evaluación conjunta de su pertinencia y fiabilidad. Las propuestas de los compañeros pueden ser tanto confirmadas como refutadas por el resto, pero el aspecto diferencial es que se deben explicitar las razones de una u otra opción, a la vez que ofrecer alternativas. El propósito deja de centrarse en cada uno, o en lo personal, para lograr el acuerdo conjunto en relación con las ideas que se van construyendo (Gentiletti, 2012, p. 54).
1 Para Vygotsky (2012a) la característica central de las funciones elementales es que se encuentran directamente y totalmente determinadas por los estímulos provenientes del entorno, mientras que en las funciones superiores, el rasgo principal es la estimulación autogenerada, la creación y uso de estímulos artificiales que se convierten en las causas inmediatas de la conducta.
“Esto es un hecho, y, como sabemos,
los hechos son difíciles de refutar”
Vygotsky, 1934/1995, p. 210
La implementación de la hoja de fórmulas, como recurso didáctico construido en forma colaborativa en clase, es posible analizarlo desde dos niveles como artefacto semiótico (Radford, 2018 citado en D’Andrea, 2019b): un nivel objetivo o conceptual, referido a las relaciones entre signos que provienen de la manera en que los conceptos matemáticos están relaciones entre sí; y un nivel vivencial o subjetivo, que tiene que ver con la relación subjetiva con la Matemática y a los signos que van dejando traza de ella.
Si bien en el apartado anterior se ha iniciado con la descripción objetiva de la hoja de fórmulas, es importante destacar que en general las hojas diseñadas daban cuenta de una desconexión entre los bloques temáticos (véase ANEXO donde se comparte un extracto de la hoja de fórmulas diseñada conjuntamente). Se pudo observar cómo se diferenciaron las fórmulas encuadrándolas en sectores, generando la poca funcionalidad que podría brindar escribir un esquema (por ejemplo: una red conceptual, diagrama de Venn, cuadro sinóptico) para repensar como los objetos matemáticos guardan relaciones, semejanzas y diferencias.
En la insistencia de los estudiantes por incluir todas las fórmulas, no olvidar ninguna “por las dudas” y aun reconociendo que “nunca se las utilizó”, y separarlas en distintos cuadros, refleja la falta de comprensión en la interrelación que guardan estos objetos matemáticos. Por ejemplo, en el caso de las fórmulas asociadas a las rectas en el plano y en el espacio tridimensional, podrían reducirse notablemente el mencionarlas a todas si se establecen y comprenden las similitudes de las expresiones que conforman esas fórmulas. Y lo mismo, podría evitarse incluir todas las nuevas fórmulas sobre cónicas porque reaparecen en superficies.
Para describir un análisis vivencial del artefacto, el trabajo en el aula se centró en la resolución grupal de actividades, y abordaje de las guías de estudio seleccionando actividades en un orden diferente con el que la cátedra las diseño con anterioridad. Estas modificaciones en el desarrollo de las clases (que con frecuencia se reducían a clase expositivas y a resolución de consignas desconectas entre sí) responden al intento de lograr los objetos asociados a las competencias mencionas en el Tabla 1.
Asimismo, para profundizar en el análisis subjetivo de la propuesta, se llevó adelante una encuesta a 101 estudiantes de cuatro cursos distintos en los que se implementó la propuesta.
Considerando que, si bien la hoja de fórmulas se armó inicialmente en grupo, para la instancia de parcial se acordó que podría cada estudiante realizar algún agregado y/o modificación; y se pueda personalizar el instrumento. De esta manera, una de las preguntas de la encuesta fue si se realizaron modificaciones a la hoja grupal, obteniéndose 63% con respuesta afirmativa. Entre las razones de esta elección, se comparten: “considero que faltaban algunas fórmulas”, “rescribir alguna de ellas cambiando el nombre de parámetros o variables”, “expresar otros despejes de las fórmulas dadas”.
Frente al interrogante sobre la utilidad del material en el parcial, un 85% responde afirmativamente y, dentro del 15% de la respuesta negativa, algunos comentarios realizados fueron: “con lo practicado ya recordaba las fórmulas”, “no la necesité porque me había preparado bien parar el examen”, “fue útil para superficies, el resto no lo pude utilizar porque no logré comenzar a desarrollar los ejercicios por su dificultad”, “no pude resolver el parcial”.
Tratando de enumerar motivos similares ante la respuesta afirmativa a la utilidad del artefacto y en función al epígrafe del presente apartado, se han reconocido al menos siete razones significativas que se comparten en la Figura 2.
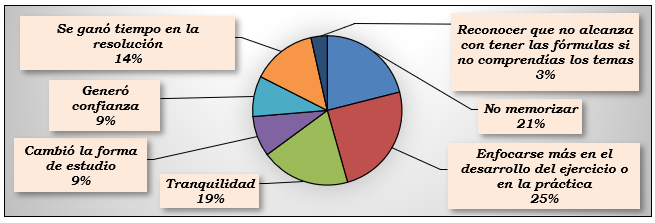
Figura 2: Motivos de la respuesta afirmativa por la utilidad de la hoja de fórmulas sobre 57 (cincuenta y siete) respuestas. Fuente: creación propia.
“Es el propio hombre el que determina su
comportamiento con ayuda de estímulos-medios
artificialmente creados”
Vygotsky, 2012c, p. 77
Haber elegido una perspectiva sociocultural como marco teórico, que acompaña el desarrollo de competencias, se sustenta en uno de los orígenes del concepto de competencia que Tobón (2006) recupera de la psicología cultural, cuyo principal representante es Vygotsky: “acciones situadas que se definen en relación con determinados instrumentos mediadores” (p. 3).
La implementación de una hoja de fórmulas como artefacto semiótico de “memoria externa” responde al principio de la significación que describe Vygotsky (2012c) al considerar que cuando “el hombre introduce estímulos artificiales, confiere significado a su conducta y crea con la ayuda de los signos, actuando desde fuera, nuevas conexiones en el cerebro” (p. 85) influyendo en el comportamiento.
Se puede observar que el uso del instrumento orientador, cuando es introducido (en el sentido vygotskyano y según el epígrafe de esta sección) en la actividad por parte del estudiante, restructura los procesos psicológicos superiores de los sujetos tales como la memoria, la atención voluntaria, la apercepción (Vygotsky, 2012a; 2012c).
La actualización de los saberes matemáticos asociados al Álgebra y Geometría Analítica, en particular el conocimiento de las nociones geométricas que se trabajan, y que Vygotsky (2012d) denomina proceso de enraizamiento (“interiorización” de las operaciones con signos) no es puramente mecánico, no se efectúa automáticamente. Se trata de un proceso complejo y mediato que inicialmente surge en el proceso de cooperación e interacción social, debido a que las funciones psicológicas superiores tienen al principio un carácter de actividad exterior (proceso interpsicológico), “el signo es, por regla general, un estímulo auxiliar externo, un medio externo de autoestímulo” (Vygotsky, 2012d, p. 79).
Se concluye que es imprescindible diseñar la hoja de fórmulas en una labor conjunta que responda a esa primera noción de objetivación: la objetivación del saber consiste en reconocer que un objeto (no sólo objetos materiales sino también el sistema de ideas científicas, artísticas, médicas, u otras) nos ob-jeta, porque no es el resultado de nuestras acciones, responde a la labor de las generaciones que nos preceden, y está impregnado de significados, y para reconocer esa “inteligencia” depositada en el objeto, Radford (2014) afirma que es necesario pasar por la objetivación definida como “el proceso social, corpóreo y simbólicamente mediado de toma de conciencia y discernimiento crítico de formas de expresión, acción y reflexión constituidas históricamente y culturalmente” (p. 141).
Para lograr la interiorización, la propia operación con signos varía, dejando de ser externa para transformarse en una capa intrapsicológica nueva, una complicada reorganización de toda la estructura de las funciones psicológicas. Vygotsky (2012c) describe tres tipos de arraigo, que podemos ejemplificarlos a través del análisis objetivo y subjetivo de la implementación de la hoja de fórmulas mencionado anteriormente.
Un primer tipo de interiorización se denomina “arraigo tipo sutura”, pensando en la sutura del tejido vivo mediante un hilo que luego cicatrizará, y el hilo provisorio se extrae. Se entiende que diseñar una hoja con las fórmulas bajo un título o subtítulo, ordenadas, diferenciadas y sin conexión separadas por cuadros son ejemplos de esa “sutura” conceptual de los saberes. La pregunta que surge, entonces, e invita a reflexionar es: ¿durante la resolución de ejercicios, se ha podido “quitar” ese hilo provisorio?
El segundo tipo de arraigo se lo llama “arraigo completo” y refiere al paso de la operación donde se borra la diferencia entre los estímulos externos y los internos. En la presente experiencia puede reconocerse esta interiorización, cuando las/os estudiantes expresan que no recurrieron a la hoja de fórmulas, porque las recordaban y podían aplicarlas sin temor a cometer errores. El interrogante que se desprende, para profundizar en la propuesta, es: ¿se trata de una “simple memorización” de la fórmula o se ha alcanzado la compresión y conocimiento de la misma?
Y el tercer tipo de arraigo se describe como “asimilación de la propia estructura del proceso”, donde se reconocen las reglas de utilización de los signos externos, se materializa el conocimiento de la propia estructura de estos últimos. En el presente caso, puede percibirse esta interiorización en respuestas tales como no alcanza con tener las fórmulas, es necesario haber logrado el conocimiento de los saberes, era necesario establecer mayor conexión entre las distintas fórmulas porque los temas están íntimamente relacionados, se puede no recurrir a la hoja porque no sólo se recuerdan algunas de ellas, sino que se podrían deducir las que no se recuerden.
Finalmente, a través del presente trabajo se ha podido “mover” de la comunicación a la metacomunicación: “del ‘aprender sobre las cosas’ al ‘aprender sobre el aprender’” (Gvirtz y Palamidessi, 2014, p. 128). En efecto, debido a ello, para mejorar futuras implementaciones de hojas de fórmulas que pueda abarcar mayor número de competencias genéricas: “competencias tecnológicas” (CONFEDI, 2014-2016), se propone:
*Trabajar el diseño de la hoja colaborativamente desde el inicio de clases, implementando mejores herramientas tecnológicas a través del aula del Campus Virtual de FRA-UTN: Google Drive, Padlet, Cmap Tools, Google Drawings, Wikis, VoiceThread, entre otros escenarios colaborativos posibles; con el fin de organizar una sesión en la que cada integrante pueda, de manera libre, compartir ideas y visualizar relaciones entre ellas. Asimismo, trabajar en un documento donde se posibilita editar, comentar, consultar, negociar conceptos y poder reconocer cambios a medida que transcurre el tiempo.
*Proponer e incentivar a realizar diferentes modelos de hojas de fórmulas: mapas conceptuales, red conceptual, cuadro sinóptico, cuadros de doble entrada; que permitan y fortalezcan las conexiones (o no) entre los saberes.
*Revisar y reformular (en caso de requerirse) las estrategias didácticas y los materiales didácticos como las guías teórico-prácticas de la cátedra, de manera tal que se orienten en la misma dirección sobre la integración genuina de los saberes, superen las desconexiones con que suelen trabajarse las unidades temáticas de la materia, en particular el bloque referido a la Geometría Analítica.
Baquero, R. (1997). Vygotsky y el aprendizaje escolar. Buenos Aires: Aique Grupo Editor.
Baquero, R. y Limón Luque, M. (2014). Introducción a la psicología del aprendizaje escolar. Bernal: UNQ Editorial.
CONFEDI (2014). Competencias en ingeniería. Argentina: Universidad FASTA.
CONFEDI (2016). Competencias y perfil del Ingeniero Iberoamericano, formación de profesores y desarrollo tecnológico e innovación. Bogotá, Colombia: ASIBEI.
CONFEDI (2018). Propuesta de estándares de segunda generación para la acreditación de carreras de ingeniería en la república argentina - Libro rojo. Argentina: CONFEDI.
D’Andrea, L. J. (2019a). Un diseño de actividades matemáticas para el desarrollo de competencias en las carreras de Ingeniería. Revista digital El enfoque por competencia en las Ciencias Básicas (CIIE – CONFEDI); 1, 125-136.
D’Andrea, L. J. (2019b). El rol dinámico de una hoja de signos en la actividad matemática. Novedades Educativas; 344, 62-68.
Daniels, H. (2003). Vygotsky y la pedagogía. Buenos Aires: Editorial Paidós.
Gentiletti, M. G. (2012). Construcción colaborativa de conocimientos integrados. Aportes de la psicología cultural en las prácticas de la enseñanza. Buenos Aires: Ediciones Novedades Educativas.
Hernández Rojas, G. (1988). Paradigmas en psicología de la educación. México: Paidós.
Moll, L. (1993). Vygotsky y la educación. España: Aique Grupo Editor.
Perrenoud, P. (2009). Enfoque por competencias ¿una respuesta al fracaso escolar? Pedagogía Social. Revista Interuniversitaria; 16, 45-64.
Radford, L. (2000). Sujeto, objeto, cultura y la formación del conocimiento. Educación Matemática; 12(1), 51-69.
Radford, L. (2006). Semiótica cultural y cognición. En R. Cantoral y O. Covián (eds.), Investigación en Matemática Educativa en Latinoamérica. México.
Radford, L. (2014). De la teoría de la objetivación. Revista Latinoamericana de Etnomatemática; 7(2), 132-150.
Radford, L. y D’Amore, B. (2017). Enseñanza y aprendizaje de las Matemáticas: problemas semióticos, epistemológicos y prácticos. Bogotá: UFD Editorial.
Tobón, S. (2006). Aspectos básicos de la formación basada en competencias. Talca: Proyecto Mesesup.
Tobón, S. (2013). Formación integral y competencias. (4ta. Ed.). Bogotá: ECOE.
Vygotsky, L. S. (1934/1995). Pensamiento y lenguaje. Buenos Aires: Editorial Paidós.
Vygotsky, L. S. (2012a). El desarrollo de los Procesos Psicológicos Superiores. Barcelona (España): Austral.
Vygotsky, L. S. (2012b). Obras escogidas – III. Madrid (España): Machado Libros.
Vygotsky, L. S. (2012c). Obras escogidas – IV. Madrid (España): Machado Libros.
Vygotsky, L. S. (2012d). Obras escogidas – VI. Madrid (España): Machado Libros.
Wertsh, J. (1988). Vygotsky y la formación social de la mente. Buenos Aires: Paidós.


