Dios creó los números naturales, los matemáticos hicieron el resto… ¿y los profesores? Consecuencias de la aritmetización del Análisis Matemático en textos universitarios.
God created natural numbers, mathematicians did the rest. But what about professors? Consequences of the arithmetization of analysis in university texts.
Sebastián José NievasLa Matemática se caracteriza por emitir juicios universales y necesarios, esto es, teoremas que se cumplen en todos los casos particulares y que no pueden darse de otra manera. Para Dou (1974) tales características se obtienen por la precisión en las definiciones y en la aplicación rigurosa de sus métodos.
Previo al siglo XIX, el Análisis Matemático se veía como un conjunto de herramientas con implicaciones prácticas extraordinarias, pero basadas en intuiciones, suposiciones y conceptos informales como cantidades infinitamente pequeñas y sumas infinitas.
Los matemáticos del siglo XIX lograron culminar la Aritmetización del Análisis, proceso que consistió en reexpresar todos los conceptos y métodos del informal Análisis Matemático en términos de la sólida Aritmética y que Kronecker resume positivamente con su célebre frase “Dios creó a los números naturales, todo lo demás es obra de los hombres”, con la intención de otorgarle así la fundamentación necesaria para garantizar las características de universalidad y necesariedad de sus teoremas.
En el presente artículo se analizan las diferentes maneras de formalizar las nociones de función y de número real, conceptos fundamentales en el proceso de Aritmetización, para luego examinar la influencia de este proceso en textos universitarios mediante la observación de libros y apuntes de cátedra de asignaturas de la Universidad Nacional del Noroeste de la Provincia de Buenos Aires (UNNOBA).
Además de los tipos de definiciones usadas en cada texto, se estudia también el orden en que se presentan los conceptos y la intensidad con la que cada autor utiliza la Historia como recurso pedagógico.
Este análisis es relevante por un lado, en un sentido histórico, dado que intenta revalorizar los esfuerzos de varios matemáticos que se ocuparon de fundamentar esta importante rama de la Matemática, además, también en un ámbito histórico, continúa la revisión bibliográfica que realizó Hermann Hankel en el año 1870 y, por último, desde el punto de vista académico, el análisis de los apuntes de cátedra de la UNNOBA y la comparación con otros libros puede ofrecer información importante para mejorar la toma de decisiones sobre la bibliografía utilizada.
El Análisis Matemático es una rama de la Matemática caracterizada por métodos infinitesimales donde los procesos de diferenciación e integración son protagonistas. Límites, continuidad, derivadas, integrales, series y sucesiones son conceptos que ocupan al estudio del Análisis Matemático.
Los orígenes del Análisis
Expresa García Venturini (2003) que el Análisis Matemático, tal como se lo conoce actualmente, es el resultado de un largo proceso de acumulación y asimilación teórica de conceptos del Cálculo Diferencial, del Cálculo Integral y de la teoría de Series.
Tal proceso encuentra sus inicios en la antigua Grecia con las figuras de Zenón de Elea, Eudoxo de Cnido y Arquímedes de Siracusa, al plantear y resolver problemas que involucran conceptos infinitesimales como lo es el método de exhaución para el cálculo de áreas y volúmenes.
Según indican Rey Pastor y Babini (2013), las consideraciones de índole infinitesimal se retoman en tiempos medievales con la introducción del cero, la regla de Merton y los estudios sobre series convergentes por parte de Oresme y Calculator.
La utilización de los efectivos y versátiles métodos infinitesimales por parte de hombres de ciencia del siglo XVII, como Cavalieri, Pascal, Fermat, Wallis y Barrow, no solo en la resolución de problemas matemáticos, sino también en áreas como Mecánica, Física y Astronomía, produjo un crecimiento sostenido del cuerpo de conocimientos de esta incipiente e informal disciplina (Rey Pastor y Babini., 2013).
Se adjudica a Newton y a Leibniz la invención del Cálculo infinitesimal, origen del moderno Análisis Matemático, debido a que a finales del siglo XVII ofrecieron una generalización y unificación de los conceptos y métodos infinitesimales conocidos hasta entonces, basada en una certera y profunda intuición, aunque sin un rigor matemático absoluto (Dou, 1974).
Ya en el siglo XVIII, debido a las producciones de matemáticos como Euler y Lagrange, “el Análisis Matemático logró un desarrollo extraordinario pero ese desarrollo, puramente formal y algorítmico, no estaba fundado sobre sistema conceptual riguroso alguno” (Rey Pastor y Babini, 2013, p. 143). No tardaron en aparecer situaciones, en apariencia paradójicas o inconsistentes, que daban cuenta de esta falta de rigor en el área. La manipulación de series sin referencia a su convergencia o divergencia, la presentación de funciones mediante series trigonométricas y las definiciones de función, derivada e integral no satisfacían los requerimientos de precisión de la época (Bergé, 2004).
Los Fundamentos del Análisis Matemático
Expresa Dou (1974) que fue en el siglo XIX cuando los matemáticos reflexionan sobre los fundamentos del Análisis y lo reconstruyen con todo rigor evitando recurrir a intuiciones geométricas a la hora de justificar los procedimientos.
En este período, los matemáticos Bolzano y Cauchy, entre otros, proponen que los principios de la disciplina se asienten sobre una base clara y firme como lo es la Aritmética (Rey Pastor y Babini, 2013). La consigna es simple: se deben expresar todos los conceptos y resultados del Análisis Matemático en términos de la Aritmética. La tarea es complicada: existe un gran arraigo a la interpretación geométrica, los procedimientos utilizados son difusos y los conceptos utilizados son insuficientes para la épica misión.
Se conoce popularmente como Aritmetización del Análisis al extenso proceso de elucidación de los objetos y procedimientos del Análisis Matemático, donde se pueden destacar los trabajos de Cauchy, Abel, Jacobi, Riemann, Dedekind, Dirichlet, Weierstrass, Cantor y Hilbert en la reformulación de los conceptos de número real, función, límite, continuidad, integral, derivada, convergencia sucesión y serie.
Para Dou (1974) resultan relevantes y de especial interés, desde la perspectiva de los fundamentos de la Matemática, las propuestas ofrecidas en la formalización del concepto de función y en la de número real.
Sobre la formalización del concepto de función
La noción de función es crucial en el estudio del Análisis Matemático moderno. Las derivadas e integrales, así como el límite y la continuidad hacen referencia y se aplican a funciones matemáticas. Indica Boyer (1994) que más allá de que el concepto de función es clave en el Análisis Matemático, es posible observar en la clarificación de este concepto la tendencia a la aritmetización por parte de la comunidad matemática.
Si bien la idea de función se remonta a unos 4000 años atrás, es recién en los últimos 300 años donde la idea cobra entidad propia y tal concepto se muestra como una de las características distintivas entre las matemáticas modernas y las matemáticas clásicas.
El cálculo desarrollado por Newton y Leibniz no tenía la forma en que se ve actualmente en la universidad, no era un cálculo de funciones. Los principales objetos de estudio en el cálculo del siglo XVII eran las curvas.
Ya en el siglo XVII, Euler afirma que el análisis matemático es la ciencia general de las variables y sus funciones y ofrece, en el año 1748, una primera definición precisa del concepto de función como una expresión analítica, es decir, una fórmula (Kleiner, 1989).
Kleiner (1989) expresa que los trabajos de Fourier de principio del siglo XIX, sobre representación mediante series trigonométricas, consideraban a las funciones como fórmulas de la forma y=f(x). Es en el estudio de las condiciones de existencia de tales series cuando Dirichlet propone, en el año 1829, la definición más general de función como una correspondencia entre conjuntos de números.
Hermann Hankel describe con claridad, en el año 1870, la situación de la definición de función en los libros de textos de esa época:
De este modo ha surgido una sensible laguna en los conceptos fundamentales del análisis, la cual, aunque todos la pasan por alto en silencio, no por eso deja menos de existir. Lo demuestra una mirada incluso a los mejores textos de análisis. Uno define la función esencialmente siguiendo a Euler; el segundo requiere que y tiene que variar con x de acuerdo con una ley, sin que se dé una explicación de este oscuro concepto; el tercero la define como Dirichlet; el cuarto no la define en absoluto. Pero todos derivan de su concepto consecuencias, que no están en él contenidas (Dou, 1974, p. 53).
Es necesario agregar, a las definiciones expuestas anteriormente, la ofrecida por parte del grupo Bourbaki en el año 1939 como una relación especial entre dos conjuntos arbitrarios (Díaz, 2013).
Sobre la formalización del concepto de número real
El concepto aceptado de número real hasta mediados del siglo XIX era el de una expresión decimal indefinida (Rey Pastor et al., 1963). Esta definición de número permitía distinguir a las expresiones periódicas de las no periódicas y considerar al conjunto R, conjunto de todos los números reales, como la unión entre los conjuntos disjuntos Q y I. En particular, al número irracional se lo seguía llamando inconmensurable y permanecía dentro de la concepción geométrica de Eudoxo de 23 siglos de antigüedad (Rey Pastor y Babini, 2013). Dicha concepción geométrica hacía eco en muchas de las demostraciones y conceptos ya formalizados que seguían apoyándose en intuiciones geométricas como la continuidad de la recta real (Dou, 1974).
El último obstáculo para consumar la Aritmetización el Análisis fue el de formular rigurosamente el concepto de número real, tal como indica Boyer (1994), “la aritmetización plena y correcta del Análisis se hizo posible solo cuando los matemáticos entendieron que los números reales había que considerarlos como estructuras intelectuales y no como las magnitudes dadas intuitivamente heredadas de la geometría de Euclides” (p. 693).
La tarea fue completada por varios matemáticos de manera independiente, algunos motivados principalmente en ofrecer rigurosidad en sus clases, como lo es el caso de Weierstrass y Dedekind.
Se distinguen principalmente cuatro formas de conceptualizar formalmente al conjunto de los números reales:
ºmediante series convergentes y clases de equivalencia, propuesto por Weierstrass en sus cursos para la Universidad de Berlín publicado en 1872 por su alumno Kossak;
ºmediante el concepto de cortaduras ofrecido por Dedekind en el año 1872;
ºmediante sucesiones de Cauchy, propuesto por Cantor y Meray en el año 1872 que luego evolucionó a sucesiones monótonas contiguas;
ºmediante un sistema axiomático al considerar un cuerpo ordenado y completo, ofrecido por Hilbert en el año 1899.
La consumación del largo proceso de aritmetización la asegura con total convicción Henri Poincaré en el congreso internacional de matemáticos de Paris del año 1900:
El Análisis ha quedado actualmente reducido a sistemas de números enteros, relacionados entre sí por una red de relaciones de igualdad o desigualdad. Las matemáticas, decimos, han sido aritmetizadas. Podemos decir que hoy día se ha logrado un rigor absoluto (Dou, 1974, p. 58).
El Análisis Matemático en la UNNOBA
La UNNOBA cuenta, entre su extensa oferta académica, con las carreras de Ingeniería Industrial, Ingeniería Mecánica, Ingeniería en Alimentos, Ingeniería Agronómica, Ingeniería en Informática, Licenciatura en Sistemas, Licenciatura en Genética, Licenciatura en Diseño Industrial, Licenciatura en Ciencias de los Alimentos, Contador Público y Licenciatura en Administración. Todas las carreras mencionadas contienen, en sus planes de estudio, asignaturas que se nutren de temas del Análisis Matemático.
Los alumnos de las carreras del área de Económicas y los de la licenciatura en Genética cursan la asignatura Elementos de Análisis Matemático (EAM), mientras que los alumnos del resto de las carreras mencionadas, en particular todas las ingenierías, comienzan su trayectoria de materias de Análisis Matemático con la asignatura Análisis Matemático Básico (AMB). Tanto EAM como AMB cubren los primeros temas del Análisis Matemático, en ellas se trabajan los temas de funciones reales, límite y continuidad, derivada, antiderivada, integral definida, entre otros.
Los conceptos de números reales y funciones se abordan en la primera unidad de ambas materias.
Si bien el plantel docente de las materias es diferente, ambas materias ofrecen apuntes de cátedra similares y cuentan en sus programas con bibliografía que los alumnos pueden encontrar en la biblioteca de la universidad.
En consonancia con la revisión bibliográfica de libros de Análisis Matemático llevada a cabo por Hankel en 1870, en el presente trabajo se realiza un análisis análogo de los libros de texto de esta disciplina. El propósito es observar no solo el tipo de definición empleada, sino también la ubicación estratégica que se le otorga tanto al concepto de función como al de número real dentro de dichos textos.
Son objetivos de la revisión bibliográfica:
- Observar y comparar los tipos de definiciones utilizadas en los conceptos de función y número real en los libros de Análisis Matemático.
- Comparar las definiciones utilizadas en los textos de la bibliografía obligatoria con las de los apuntes de cátedra.
- Analizar críticamente la importancia asignada al proceso de Aritmetización del Análisis en los libros de texto, teniendo en cuenta el tipo de definición y la ubicación dentro del libro donde se encuentren los conceptos de función y número real.
- Concluir sobre la importancia prestada al proceso de Aritmetización del Análisis en las asignaturas EAM y AMB de acuerdo a la bibliografía obligatoria y los apuntes de cátedra (que no se consideran incluidos en la bibliografía).
Se realizó una selección de 21 libros de Análisis Matemático de diferentes autores, editoriales y años de publicación desde 1952 hasta 2018. El criterio de selección está ligado al acceso que tienen los alumnos de la UNNOBA al material, más precisamente se consideraron los ejemplares disponibles en la biblioteca de la universidad y algunos que se pueden encontrar en la web. Para libros con más de una edición, simplemente se analizó una elegida de forma arbitraria.
En la Tabla 1 se muestran, ordenados por año de publicación, todos los libros que fueron revisados. Las primeras dos columnas indican cuáles son los que componen la bibliografía de Elementos de Análisis Matemático y de Análisis Matemático Básico.

Para cada uno de los libros de la Tabla 1 y los apuntes de cátedra de EAM y AMB se observó:
• El tipo de definición del concepto de función utilizada y, para los casos que hacen explicita una definición, la ubicación dentro de la estructura del texto en la que se presenta.
• El tipo de definición del concepto de número real utilizada y, para los casos que hacen explicita una definición, la ubicación dentro de la estructura del texto en la que se presenta.
• La existencia de algún otro aspecto directamente relacionado a los fundamentos o a la historia del Análisis Matemático.
Los aspectos observados definen las siguientes variables:
• Variable 1: Tipo de definición de función. Los valores posibles de la variable 1 son: Euler, y=f(x), Dirichlet, Bourbaki, No define.
• Variable 2: Posición en el texto. Los valores posibles para los casos afirmativos de la variable 1 son los números naturales y Apéndice.
• Variable 3: Tipo de definición de número real. Los valores posibles de la variable 3 son: Axiomática, Decimal, Dedekind, Cantor, Weierstrass, No define.
• Variable 4: Posición en el texto. Los valores posibles para los casos afirmativos de la variable 3 son los números naturales y Apéndice.
• Variable 5: Frecuencia del uso de la Historia y los Fundamentos de la Matemática. Considerando el porcentaje de capítulos en los que se menciona la Historia de los conceptos. Los valores posibles son: Muy poca (menos del 25% de los capítulos), Moderada (desde el 25% hasta el 50% de los capítulos), Considerable (desde el 50% hasta el 75% de los capítulos) y Muy frecuente (al menos el 75% de los capítulos).
Al momento de definir el valor de cada variable se realizó una lectura completa y comprensiva de cada texto observando con precisión las definiciones utilizadas y el enfoque realizado por el autor. Es necesario aclarar las decisiones que se tomaron al momento de obtener los valores de las variables con la intención de evitar ambigüedades:
• En los casos que se mencionan varias posibles aproximaciones de un concepto, en particular en las variables 1 y 3, se considera lo que el autor utilice explícitamente como definición.
• Se considera que el autor hace uso de la Historia o de los Fundamentos del Análisis cuando menciona diferentes procesos históricos de formalización o cuando hace mención a un matemático. No se considera mención histórica si el autor nombra un apellido de forma descontextualizada debido a que en Matemática muchos teoremas, fórmulas y reglas se distinguen por apellidos.
• En los apuntes de cátedra no existe la división por capítulos por lo que se tomó la división por las unidades que se indican en el programa de la asignatura.
Se definieron tres grupos de libros de texto:
• Textos seleccionados: compuesto por el total de los libros de la Tabla 1;
• Bibliografía de EAM: compuesto por los libros de la bibliografía de Elementos de Análisis Matemático;
• Bibliografía de AMB: compuesto por los libros de la bibliografía de Análisis Matemático Básico.
Una vez obtenidos todos los datos, con ánimo de comparar las variables en cada uno de los grupos de libros, se realizó:
• Una tabla de frecuencias relativas para la variable 1;
• Una tabla de frecuencias relativas para la variable 3;
• Una tabla de frecuencias relativas para la comparación de las variables 2 y 4;
• Una tabla de frecuencias relativas para la variable 5.
Tipo de definición de función utilizada.
En los apuntes de cátedra tanto de EAM como de AMB, se presenta al inicio la definición de función según Dirichlet. En ambos apuntes, se establece posteriormente, que las funciones se pueden definir de la forma y = f(x).

En la Figura 1 es posible observar que todos los textos analizados definen explícitamente el concepto de función y ninguno lo hace siguiendo a Euler. Aunque una proporción razonable define siguiendo a Bourbaki, la gran mayoría de los textos se inclinan hacia la definición de Dirichlet.
Si bien se observa a simple vista que las bibliografías de EAM y AMB acompañan la tendencia del total de libros hacia las definiciones mencionadas, llama la atención que, dada la elección realizada para los apuntes de cátedra, no se observe una diferencia más pronunciada en la bibliografía de las asignaturas a favor de la definición de Dirichlet.
Tipo de definición de número real utilizada.
Tanto en los apuntes de cátedra ofrecido a los alumnos de EAM como a los de AMB, los autores optaron por no definir al número real. En la Figura 2 es posible observar una marcada tendencia por parte de los textos seleccionados hacia la definición de tipo Axiomática y a la de tipo Decimal. En este sentido la bibliografía de AMB acompaña esta tendencia. Por su parte la bibliografía de EAM parece estar ligeramente sesgada hacia la que utiliza una definición Decimal del número real.

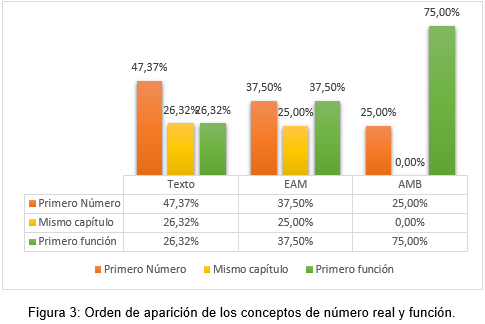
Orden en la definición de los conceptos de función y número real.
Si se considera al conjunto de textos que definen a ambos conceptos, es posible comparar el orden en los capítulos que se ofrecen las definiciones. En la Figura 3 se puede observar que aproximadamente la cuarta parte de los libros de texto presentan una definición de número real en un capítulo posterior al de función. En los seleccionados para EAM la proporción es similar a la del total, pero en la selección para AMB los textos que definen al número real en un capítulo posterior a la definición de función ascienden al 75%.
Uso de la Historia en el desarrollo de los conceptos.
Al examinar los apuntes de cátedra de AMB se observa que el 40% de las unidades hacen referencia a aspectos históricos del Análisis Matemático mientras que los apuntes de EAM lo hacen en un 33,33% de las unidades, por lo que las ambas obras encuadran en propuestas que hacen un uso moderado de la Historia y los Fundamentos del Análisis Matemático.
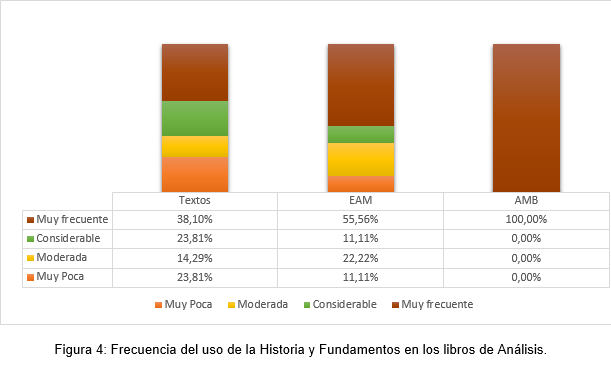
Como se puede apreciar en la Figura 4, el uso de la Historia está uniformemente distribuido en los textos seleccionados. Es destacable que, en relación a los libros utilizados en las asignaturas analizadas, más del 50% de los textos empleados en EAM hacen un uso muy frecuente de la Historia. Por otro lado, en AMB, todos los libros de la bibliografía emplean la Historia y los Fundamentos como recursos pedagógicos de manera muy frecuente.
En base a los datos recogidos es posible deducir que el proceso de Aritmetización del Análisis Matemático ha dejado ciertas huellas en los textos universitarios.
Las marcas que el proceso dejó son muy nítidas en la definición de función que se utiliza en los libros de Análisis. Se observa, en los textos seleccionados, una marcada inclinación hacia la definición de función de Dirichlet, a la cual Dou (1974) considera como la definición moderna de función, y hacia la definición de Bourbaki, grupo responsable, según Kline (1980), en la inspiración de la reforma de la Matemática Moderna que se produjo en Estados Unidos y Europa en la década de 1960. En este sentido, y a diferencia de lo expresado por Hankel, no solo la totalidad de los libros analizados se ocupan de definir el concepto, sino también de hacerlo mediante una definición formal y moderna.
No se observan consecuencias fuertes del proceso de Aritmetización en el tipo de definición de número real empleada en los textos universitarios ya que menos del 20% recurren a los métodos formales consolidados en la década del 1870 por Dedekind, Cantor y Weierstrass y que, según Rey Pastor y Babini (2013), completan el proceso de Aritmetización del Análisis. En cambio, se puede observar que los libros de texto revisados se inclinan más bien, en proporciones similares, hacia las definiciones Axiomática, postura que se acerca más a la formalización que propone el grupo Bourbaki, y a la Decimal clásica, e informal, de Eudoxo.
Tampoco se observa una gran influencia de la Aritmetización del Análisis en la distribución y orden de los contenidos expuestos en los libros de texto. Esta última afirmación se puede justificar en base a que el concepto de función se formalizó unos cuarenta años antes que el de número real y, en los libros de texto observados, menos del 30% lo hacen siguiendo tal orden. En lo referido a las asignaturas de la UNNOBA que cubren los conceptos del Análisis es posible observar que, a pesar que la muestra de libros de textos analizada tiene una amplitud de 66 años, existe una gran concentración de la bibliografía elegida en los programas de AMB y EAM en torno al año 2000. Tal concentración puede deberse a varias razones, aunque conviene señalar que los docentes que participaron en la confección de los apuntes de cátedra se encuentran ligados a la universidad desde el año 2003, año de su creación.
Tanto la bibliografía de EAM como la de AMB se muestran representativas de la población total de textos, asemejándose a un muestreo aleatorio, en lo referido al tipo de definición de función y de número real ya que las frecuencias relativas resultan similares. Por otro lado, en coherencia con los apuntes de cátedra, existe un marcado sesgo en la asignatura AMB hacia la elección de textos que respetan el orden cronológico del proceso de Aritmetización y el uso de la Historia, no así en la selección de la bibliografía de EAM.
No se cuenta con suficiente información para proponer la existencia de inconsistencias en la redacción de los apuntes de cátedra de AMB y EAM respecto de la selección de la bibliografía de la materia.
Queda pendiente, para un trabajo más amplio, aumentar la selección de textos incorporando nuevos libros, por ejemplo, posteriores al año 2018 y de otros idiomas y, para obtener conclusiones más sólidas y correlaciones entre variables, aplicar herramientas estadísticas más sofisticadas como test de hipótesis y análisis de correlación.
Bergé, A. (2004). Un estudio de la evolución del pensamiento matemático: el ejemplo de la conceptualización del conjunto de los números reales y de la noción de completitud en la enseñanza universitaria. Facultad de Ciencias Exactas y Naturales. Universidad de Buenos Aires.
Boyer, C. B. (1994). Historia de la Matemática. Madrid, España: Alianza Editorial.
Díaz, J. L. (2013). El Concepto de Función: Ideas pedagógicas a partir de su historia e investigaciones. El Cálculo y su enseñanza, 4, 13-25.
Dou, A. (1974). Fundamentos de la Matemática. (2ª ed.) Barcelona, España: Labor.
García Venturini, A. E. (2003). Los matemáticos que hicieron historia. Buenos Aires, Argentina: Ediciones Cooperativas.
Kleiner, I. (1989). Evolution of the function concept: A brief survey. The college Mathematics Journal 20(4), 282-300.
Kline, M. (1980). El fracaso de la matemática moderna ¿Por qué Juanito no sabe sumar? Madrid, España: Siglo XXI editores.
Leithold, L. (1998). El cálculo. (7ª ed.). México: Oxford University Press.
Rey Pastor, J. & Babini, J. (2013). Historia de la matemática: Del Renacimiento a la actualidad (Vol. 2). Barcelona, España: Gedisa.
Rey Pastor, J., Calleja, P. & Trejo, C. (1963). Análisis matemático (vol. 1). Buenos Aires, Argentina: Kapeluz.

